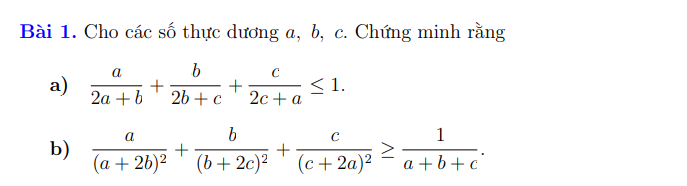a) Ta có: \(\sqrt{2018}-\sqrt{2017}=\dfrac{1}{\sqrt{2018}+\sqrt{2017}}\)
\(\sqrt{2016}-\sqrt{2015}=\dfrac{1}{\sqrt{2016}+\sqrt{2015}}\)
mà \(\dfrac{1}{\sqrt{2018}+\sqrt{2017}}< \dfrac{1}{\sqrt{2016}+\sqrt{2015}}\)
nên \(\sqrt{2018}-\sqrt{2017}< \sqrt{2016}-\sqrt{2015}\)
b) Ta có: \(\left(\sqrt{2018}+\sqrt{2016}\right)^2=4034+24\sqrt{14126}\)
\(\left(2\sqrt{2017}\right)^2=8068=4034+4034\)
mà \(24\sqrt{14126}< 4034\)
nên \(\sqrt{2018}+\sqrt{2016}< 2\sqrt{2017}\)










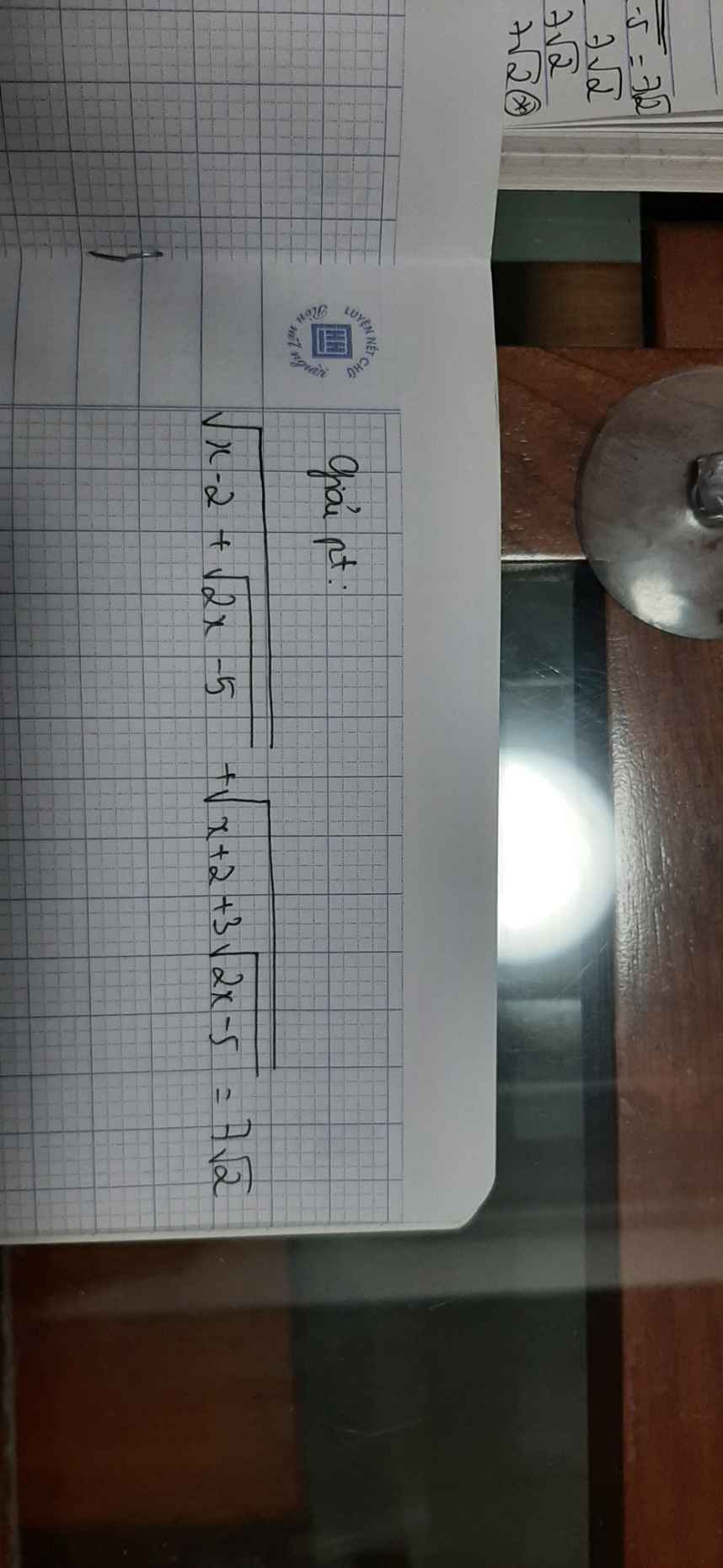

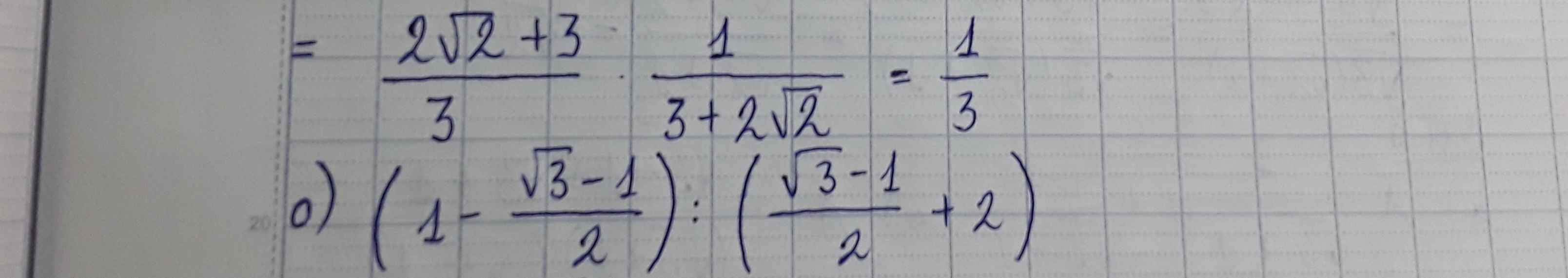 giải giúp mk câu o vs ạ
giải giúp mk câu o vs ạ