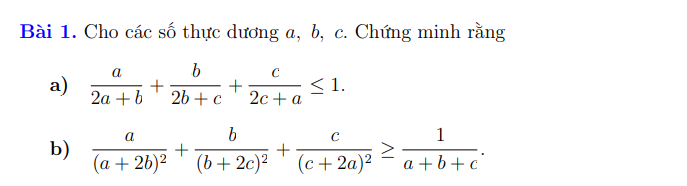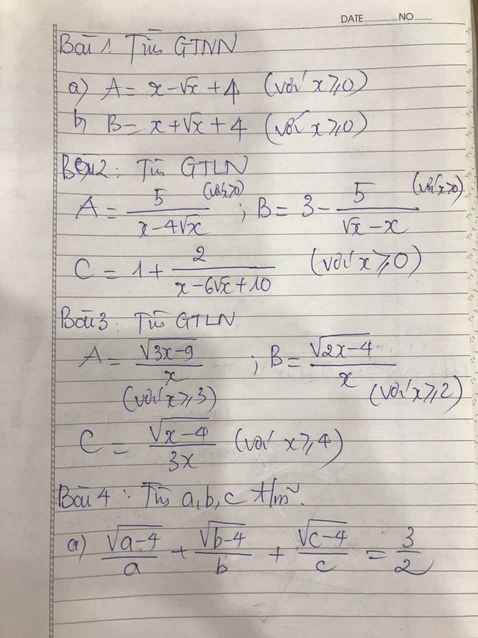c) Ta có: \(\left(4+\sqrt{15}\right)\left(\sqrt{10}-\sqrt{6}\right)\cdot\sqrt{4-\sqrt{15}}\)
\(=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{8-2\sqrt{15}}\)
\(=\dfrac{\left(8+2\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)^2}{2}\)
\(=\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2\cdot\left(\sqrt{5}-\sqrt{3}\right)^2}{2}\)
\(=\dfrac{\left(5-3\right)^2}{2}=\dfrac{2^2}{2}=2\)









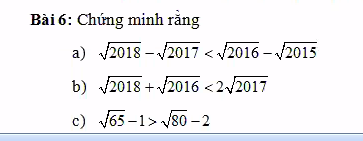

 Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.
Các bạn ơi giúp mk với. Mk cần gấp lắm ạ.Các bạn giải chi tiết giúp mk nhé . Mk hứa sẽ vote 5* cho . Mk cảm ơn nhiều.


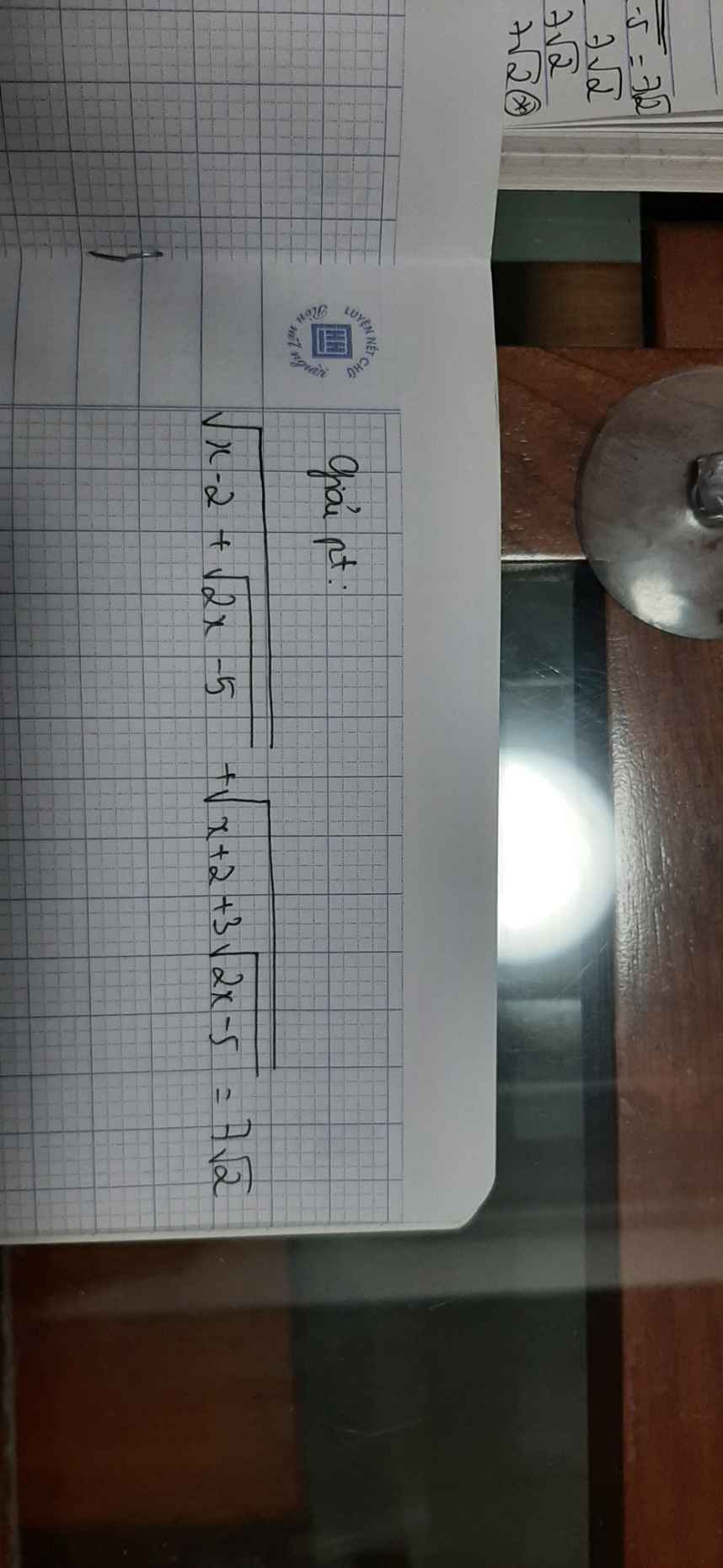

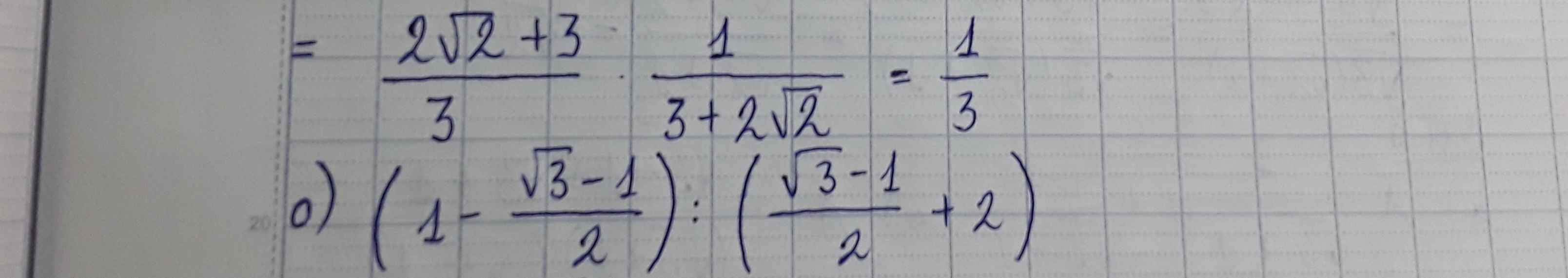 giải giúp mk câu o vs ạ
giải giúp mk câu o vs ạ