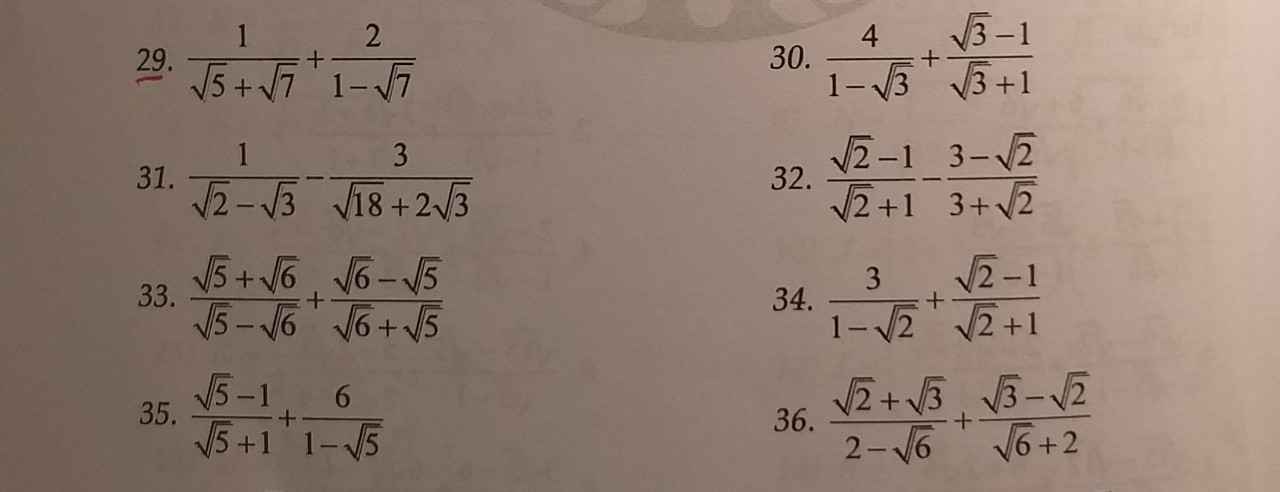Question

anh e giúp mik mấy câu này vs! sau đợt nghỉ dịch này chắc não ko còn j. NHANH NHÁ, MIK ĐAG CẦN GẤP!

Answer 1

29: Ta có: \(\dfrac{1}{\sqrt{7}+\sqrt{5}}+\dfrac{2}{1-\sqrt{7}}\)

\(=\dfrac{\sqrt{7}-\sqrt{5}}{2}-\dfrac{2\sqrt{7}-2}{6}\)

\(=\dfrac{3\sqrt{7}-3\sqrt{5}-2\sqrt{7}+2}{6}\)

\(=\dfrac{-3\sqrt{5}-2}{6}\)

30: Ta có: \(\dfrac{4}{1-\sqrt{3}}+\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\)

\(=\dfrac{-4\sqrt{3}-4}{2}+\dfrac{4-2\sqrt{3}}{2}\)

\(=\dfrac{-4\sqrt{3}-4+4-2\sqrt{3}}{2}=-3\sqrt{3}\)

31: Ta có: \(\dfrac{1}{\sqrt{2}-\sqrt{3}}-\dfrac{3}{\sqrt{18}+2\sqrt{3}}\)

\(=-\sqrt{3}-\sqrt{2}-\dfrac{3}{3\sqrt{2}+2\sqrt{3}}\)

\(=-\sqrt{3}-\sqrt{2}-\dfrac{9\sqrt{2}-6\sqrt{3}}{6}\)

\(=\dfrac{-6\sqrt{3}-6\sqrt{2}-9\sqrt{2}+6\sqrt{3}}{6}=\dfrac{-15\sqrt{2}}{6}\)

\(=\dfrac{-5\sqrt{2}}{2}\)

Answer 2

29.

\(=\frac{\sqrt{7}-\sqrt{5}}{(\sqrt{7}-\sqrt{5})(\sqrt{7}+\sqrt{5})}+\frac{2(1+\sqrt{7})}{(1-\sqrt{7})(1+\sqrt{7})}\)

\(=\frac{\sqrt{7}-\sqrt{5}}{7-5}+\frac{2(1+\sqrt{7})}{1-7}=\frac{\sqrt{7}-\sqrt{5}}{2}-\frac{1+\sqrt{7}}{3}=\frac{\sqrt{7}-3\sqrt{5}-2}{6}\)

Answer 3

30.

\(=\frac{4(1+\sqrt{3})}{(1-\sqrt{3})(1+\sqrt{3})}+\frac{(\sqrt{3}-1)^2}{(\sqrt{3}+1)(\sqrt{3}-1)}=\frac{4(1+\sqrt{3})}{1-3}+\frac{4-2\sqrt{3}}{3-1}\)

\(=\frac{4(1+\sqrt{3})}{-2}+\frac{4-2\sqrt{3}}{2}=-2(1+\sqrt{3})+2-\sqrt{3}=-3\sqrt{3}\)

Answer 4

31.

\(=\frac{\sqrt{2}+\sqrt{3}}{(\sqrt{2}+\sqrt{3})(\sqrt{2}-\sqrt{3})}-\frac{3(\sqrt{18}-2\sqrt{3})}{(\sqrt{18}+2\sqrt{3})(18-2\sqrt{3})}=\frac{\sqrt{2}+\sqrt{3}}{2-3}-\frac{3(18-2\sqrt{3})}{6}\)

\(=-(\sqrt{2}+\sqrt{3})-(9-\sqrt{3})=-\sqrt{2}-9\)

Answer 5

32.

\(=\frac{(\sqrt{2}-1)^2}{(\sqrt{2}-1)(\sqrt{2}+1)}-\frac{(3-\sqrt{2})^2}{(3-\sqrt{2})(3+\sqrt{2})}=\frac{3-2\sqrt{2}}{2-1}-\frac{11-6\sqrt{2}}{3^2-2}\)

\(=3-2\sqrt{2}-\frac{11-6\sqrt{2}}{7}=\frac{10-8\sqrt{2}}{7}\)

Answer 6

33.

\(=\frac{(\sqrt{5}+\sqrt{6})^2+(\sqrt{6}-\sqrt{5})(\sqrt{5}-\sqrt{6})}{(\sqrt{5}-\sqrt{6})(\sqrt{6}+\sqrt{5})}=\frac{4\sqrt{30}}{5-6}=-4\sqrt{30}\)

Answer 7

34.

\(=\frac{3(1+\sqrt{2})}{(1-\sqrt{2})(1+\sqrt{2})}+\frac{(\sqrt{2}-1)^2}{(\sqrt{2}+1)(\sqrt{2}-1)}=\frac{3(1+\sqrt{2})}{1-2}+\frac{3-2\sqrt{2}}{2-1}\)

\(=-3(1+\sqrt{2})+3-2\sqrt{2}=-5\sqrt{2}\)

Answer 8

35.

\(=\frac{(\sqrt{5}-1)(1-\sqrt{5})+6(\sqrt{5}+1)}{(\sqrt{5}+1)(1-\sqrt{5})}=\frac{2\sqrt{5}-6+6\sqrt{5}+6}{1-5}=\frac{8\sqrt{5}}{-4}=-2\sqrt{5}\)

Answer 9

36.

\(=\frac{(\sqrt{2}+\sqrt{3})(\sqrt{6}+2)+(\sqrt{3}-\sqrt{2})(2-\sqrt{6})}{(2-\sqrt{6})(\sqrt{6}+2)}\)

\(=\frac{8\sqrt{3}}{2^2-6}=\frac{8\sqrt{3}}{-2}=-4\sqrt{3}\)