Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=15cm\)
Vì AD là phân giác \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Rightarrow\dfrac{DC}{AC}=\dfrac{BD}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{DC}{AC}=\dfrac{BD}{AB}=\dfrac{15}{12+9}=\dfrac{15}{21}=\dfrac{5}{7}\Rightarrow BD=\dfrac{45}{7};CD=\dfrac{60}{7}cm\)
Xét tam giác ABC vuông tại A có DE vuông AC
=> DE // AB
Theo hệ quả Ta lét \(\dfrac{DC}{BC}=\dfrac{DE}{AB}\Rightarrow DE=\dfrac{DC.AB}{BC}=\dfrac{36}{7}cm\)
Bài 7: Chứng minh theo quy nạp:
-Khi n=3 thì mệnh đề trở thành:
\(4.5.6=120⋮2^3\)
-Giả sử mệnh đề đúng với n=k tức là:
\(\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)⋮2^k\).
-Ta chứng minh mệnh đề cũng đúng với n=k+1 tức là:
\(\left(k+2\right)\left(k+3\right)\left(k+4\right)...\left(2k\right)\left(2k+1\right)\left(2k+2\right)⋮2^{k+1}\).
-Thật vậy, ta có:
\(\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)⋮2^k\)
\(\Rightarrow2.\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)⋮2^{k+1}\)
\(\Rightarrow2.\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)\left(2k+1\right)⋮2^{k+1}\).
\(\Rightarrow\left(k+2\right)\left(k+3\right)...\left(2k\right)\left(2k+1\right)\left(2k+2\right)⋮2^{k+1}\).
-Vậy mệnh đề cũng đúng với n=k+1. Theo nguyên lý Quy nạp toán học, mệnh đề đúng với mọi n nguyên dương lớn hơn 0.
BD=\(\dfrac{45}{7}\) cm; ED=\(\dfrac{36}{7}\)cm













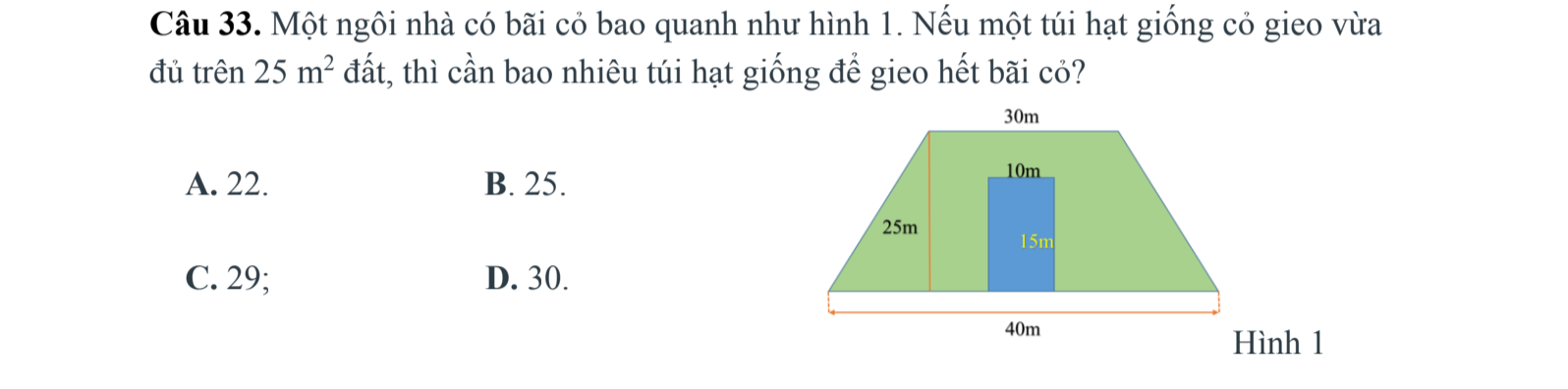
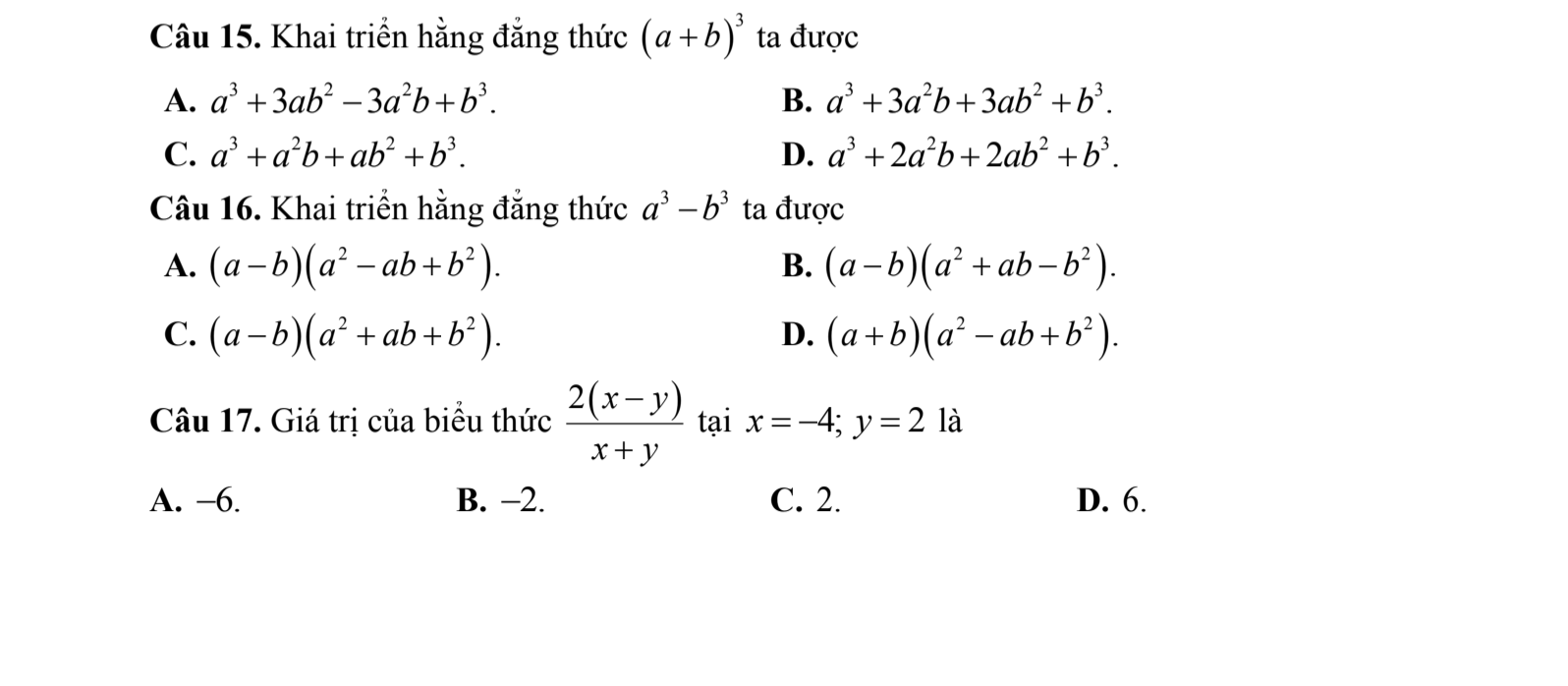


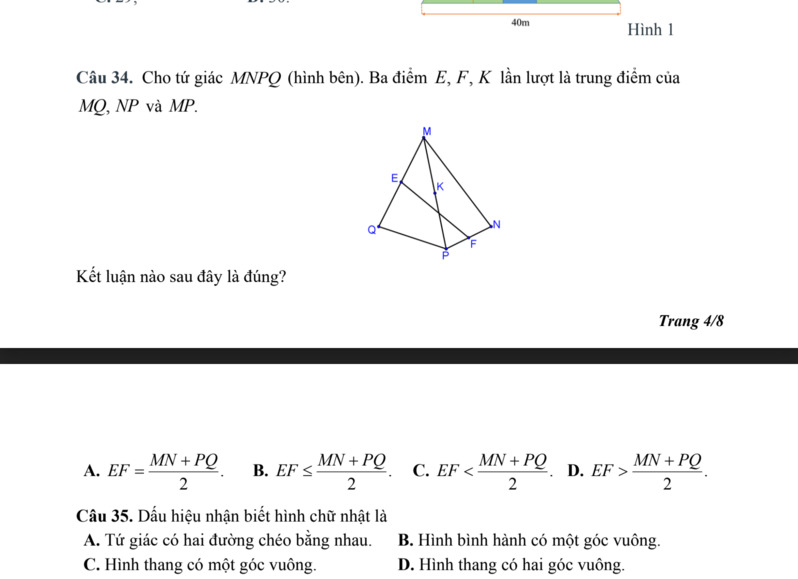

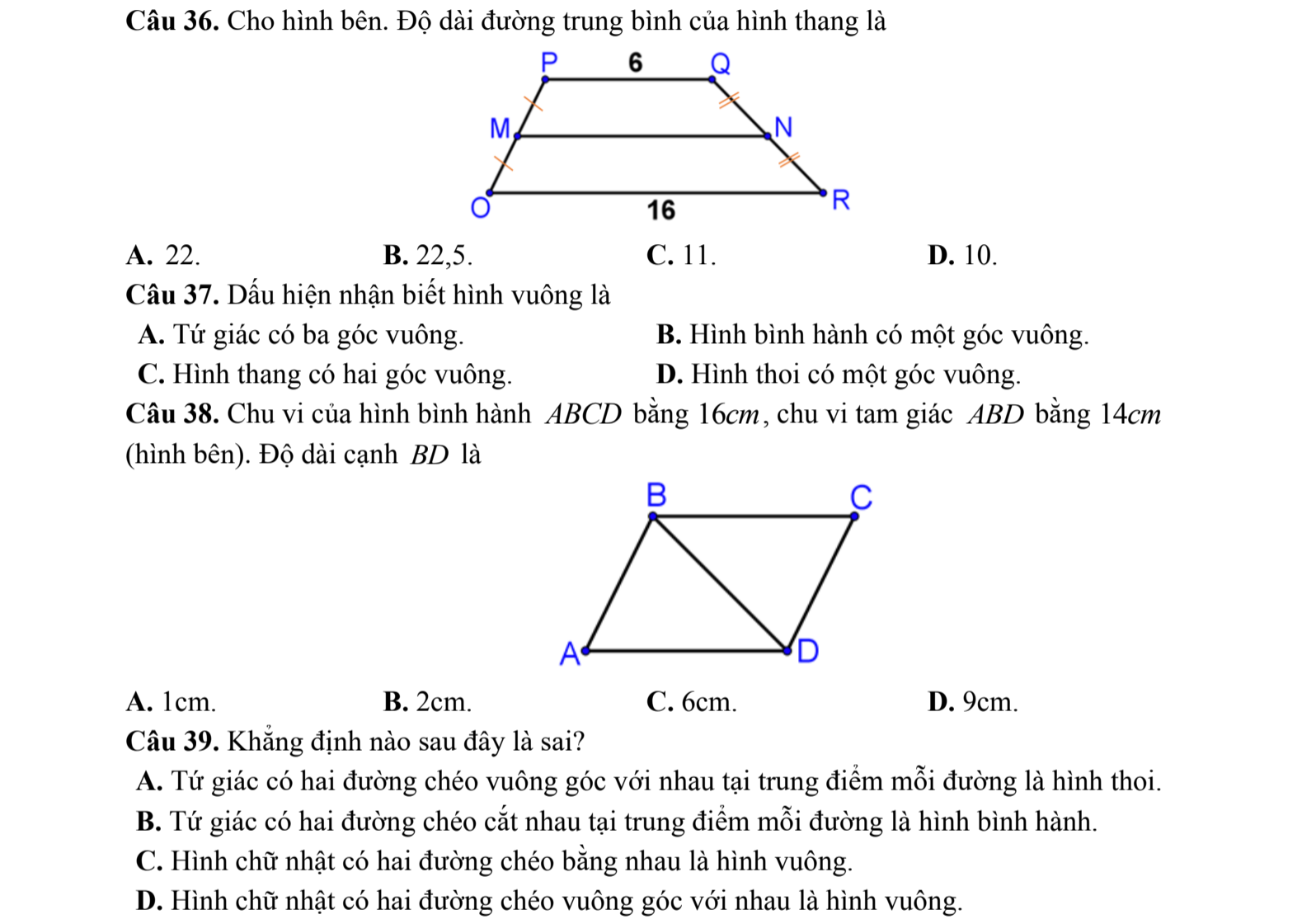


 Giúp em 45 câu trắc nghiệm này vs
Giúp em 45 câu trắc nghiệm này vs










