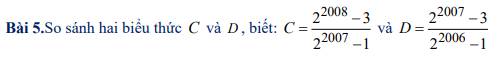Xét hiệu: \(C-D=\dfrac{2^{2008}-3}{2^{2007}-1}-\dfrac{2^{2007}-3}{2^{2006}-1}\)
\(=\dfrac{\left(2^{2008}-3\right)\left(2^{2006}-1\right)-\left(2^{2007}-1\right)\left(2^{2007}-3\right)}{\left(2^{2007}-1\right)\left(2^{2006}-1\right)}\)
\(=\dfrac{2^{4014}-2^{2008}-3\cdot2^{2006}+3-2^{4014}+3\cdot2^{2007}+2^{2007}-3}{\left(2^{2007}-1\right)\left(2^{2006}-1\right)}\)
\(=\dfrac{3\left(2^{2007}-2^{2006}\right)-\left(2^{2008}-2^{2007}\right)}{x}\) với \(x=\left(2^{2007}-1\right)\left(2^{2006}-1\right)\)
\(=\dfrac{3\cdot2^{2006}-2^{2007}}{x}\)
\(=\dfrac{3\cdot2^{2007}-2\cdot2^{2006}}{x}=\dfrac{2^{2006}}{x}\)
Dễ thấy: \(\left\{{}\begin{matrix}2^{2006}>0\\\left\{{}\begin{matrix}2^{2007}-1>0\\2^{2006}-1>0\end{matrix}\right.\Rightarrow x=\left(2^{2007}-1\right)\left(2^{2006}-1\right)>0\end{matrix}\right.\)
Nên: \(C-D=\dfrac{2^{2006}}{x}>0\Leftrightarrow C>D\).
Vậy: \(C>D.\)