a: \(\dfrac{x^4+4}{x\left(x^2+2\right)-2x^2-\left(x-1\right)^2-1}\)
\(=\dfrac{\left(x^2+2\right)^2-\left(2x\right)^2}{x^3+2x-2x^2-x^2+2x-1-1}\)
\(=\dfrac{\left(x^2-2x+2\right)\left(x^2+2x+2\right)}{x^3-3x^2+4x-2}\)
\(=\dfrac{\left(x^2-2x+2\right)\left(x^2+2x+2\right)}{x^3-x^2-2x^2+2x+2x-2}\)
\(=\dfrac{\left(x^2-2x+2\right)\left(x^2+2x+2\right)}{\left(x-1\right)\left(x^2-2x+2\right)}=\dfrac{x^2+2x+2}{x-1}\)
b: \(=\dfrac{x^2+2xy+y^2-z^2-2zt-t^2}{x^2+2xz+z^2-y^2-2yt-t^2}\)
\(=\dfrac{\left(x+y\right)^2-\left(z+t\right)^2}{\left(x+z\right)^2-\left(y+t\right)^2}\)
\(=\dfrac{x+y-z-t}{x+z-y-t}\)
c: \(=\dfrac{3y\left(1-x\right)-2\left(1-x\right)}{\left(1-x\right)\left(1+x+x^2\right)-3x\left(1-x\right)}\)
\(=\dfrac{3y-2}{1+x+x^2-3x}=\dfrac{3y-2}{\left(1-x\right)^2}\)

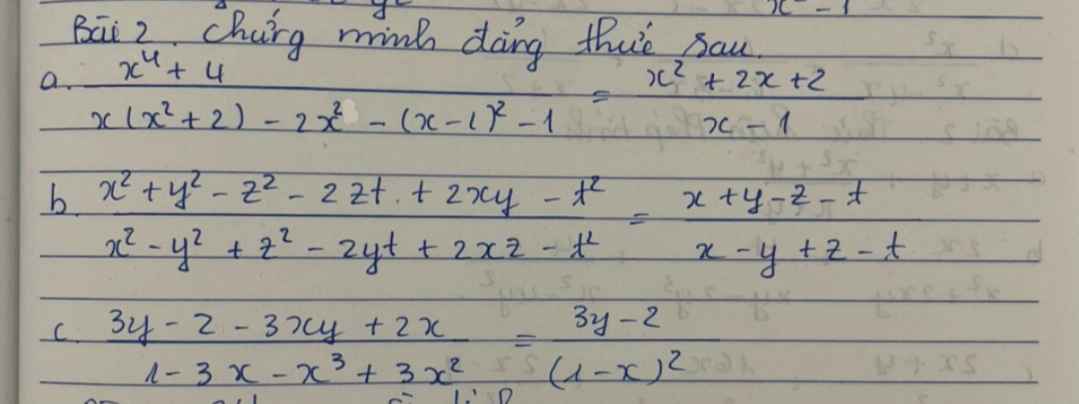

















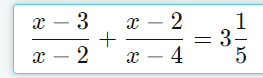 mình cần gấp giúp mình với
mình cần gấp giúp mình với