Bài 1:
\(a,=\dfrac{3x-3+4x+2+1-5x}{6x}=\dfrac{2x}{6x}=\dfrac{1}{3}\\ b,=\dfrac{x+y+2x-2y-3}{\left(x-y\right)\left(x+y\right)}=\dfrac{3x-y-3}{\left(x-y\right)\left(x+y\right)}\\ c,\dfrac{4x-8-3x-6+12}{\left(x-2\right)\left(x+2\right)}=\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x+2}\\ d,=\dfrac{x-1+x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{1}{x-1}\\ e,=\dfrac{x^2+2x+1-x^2-2x}{x\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x\left(x-1\right)\left(x+1\right)}\\ f,=\dfrac{x^2-4-x^2+10}{x+2}=\dfrac{6}{x+2}\\ g,=\dfrac{x^2-x+1-1+x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x^2+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(h,=\dfrac{x^2+9xy-3xy+9y^2}{x\left(x-3y\right)\left(x+3y\right)}=\dfrac{\left(x+3y\right)^2}{x\left(x-3y\right)\left(x+3y\right)}=\dfrac{x+3y}{x\left(x-3y\right)}\)













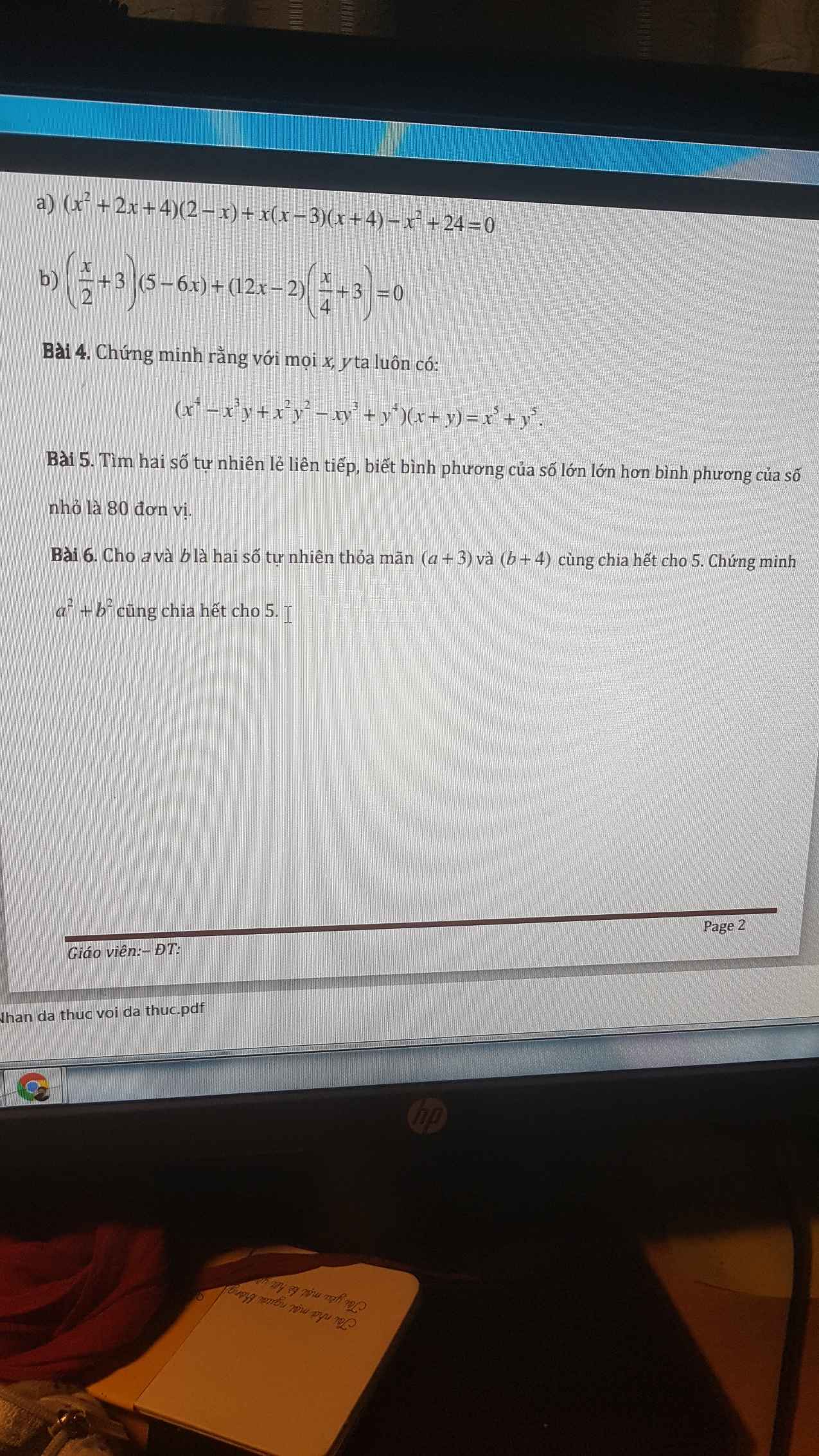

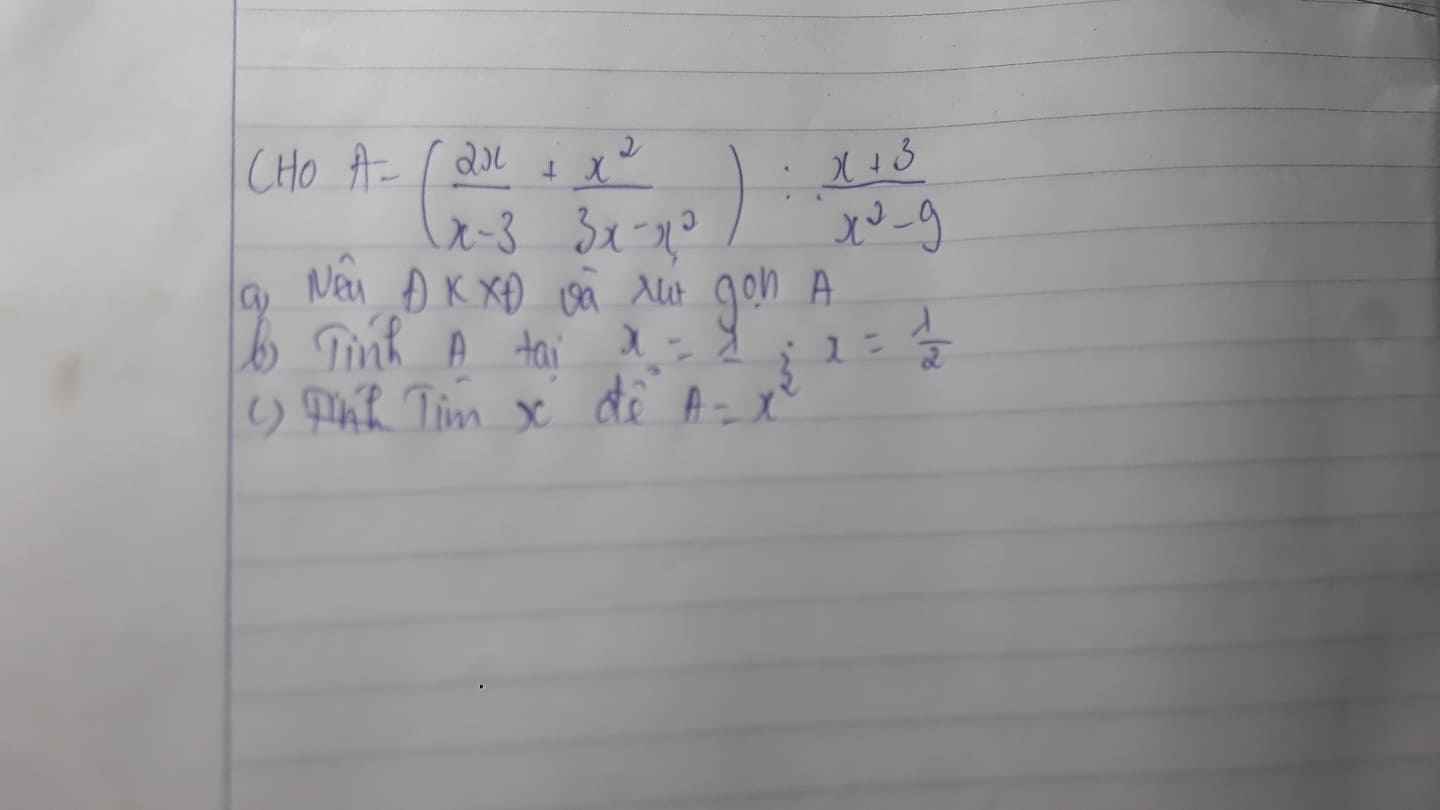



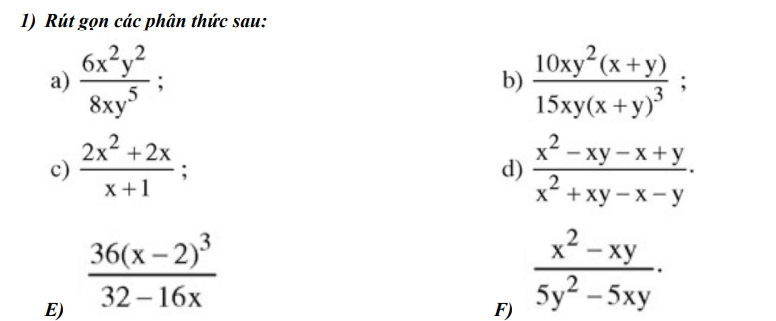

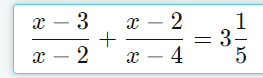 mình cần gấp giúp mình với
mình cần gấp giúp mình với