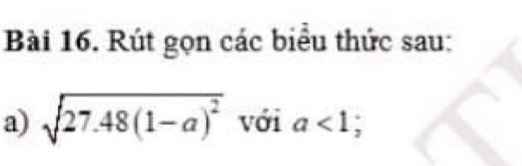Kẻ đường trung trực AH của tam giác cân ABC
\(\Rightarrow\)\(\left\{{}\begin{matrix}BH=\dfrac{1}{2}BC\\\widehat{BAH}=\widehat{HAC}=\widehat{BAC}:2=60^0\end{matrix}\right.\)
Ta có: \(AB=AC=6cm\)
Áp dụng tỉ số lượng giác trong tam giác ABH vuông tại H:
\(sinBAH=\dfrac{BH}{AB}\Rightarrow sin60^0=\dfrac{BH}{6}\Rightarrow BH=3\sqrt{3}cm\)
\(\Rightarrow BC=2BH=6\sqrt{3}\left(cm\right)\)
Ta có: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-\widehat{BAC}}{2}=30^0\)(Tam giác ABC cân tại A)






 PP
PP