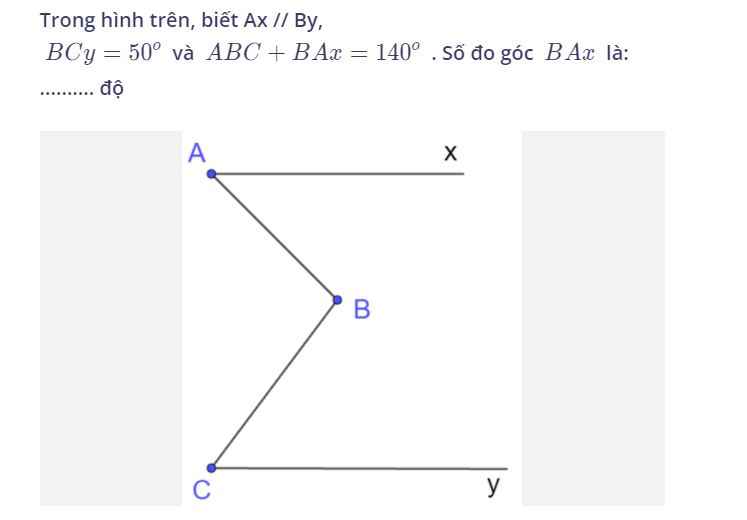
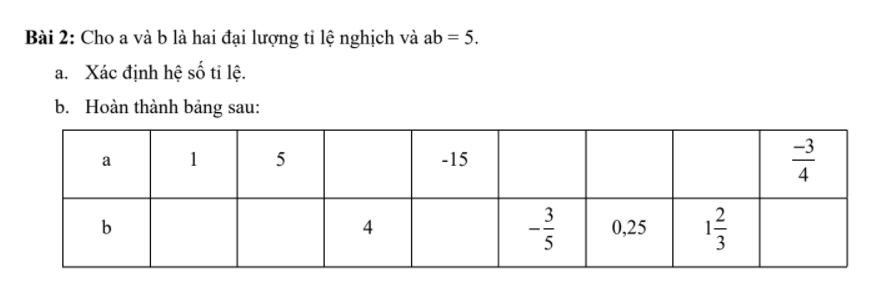
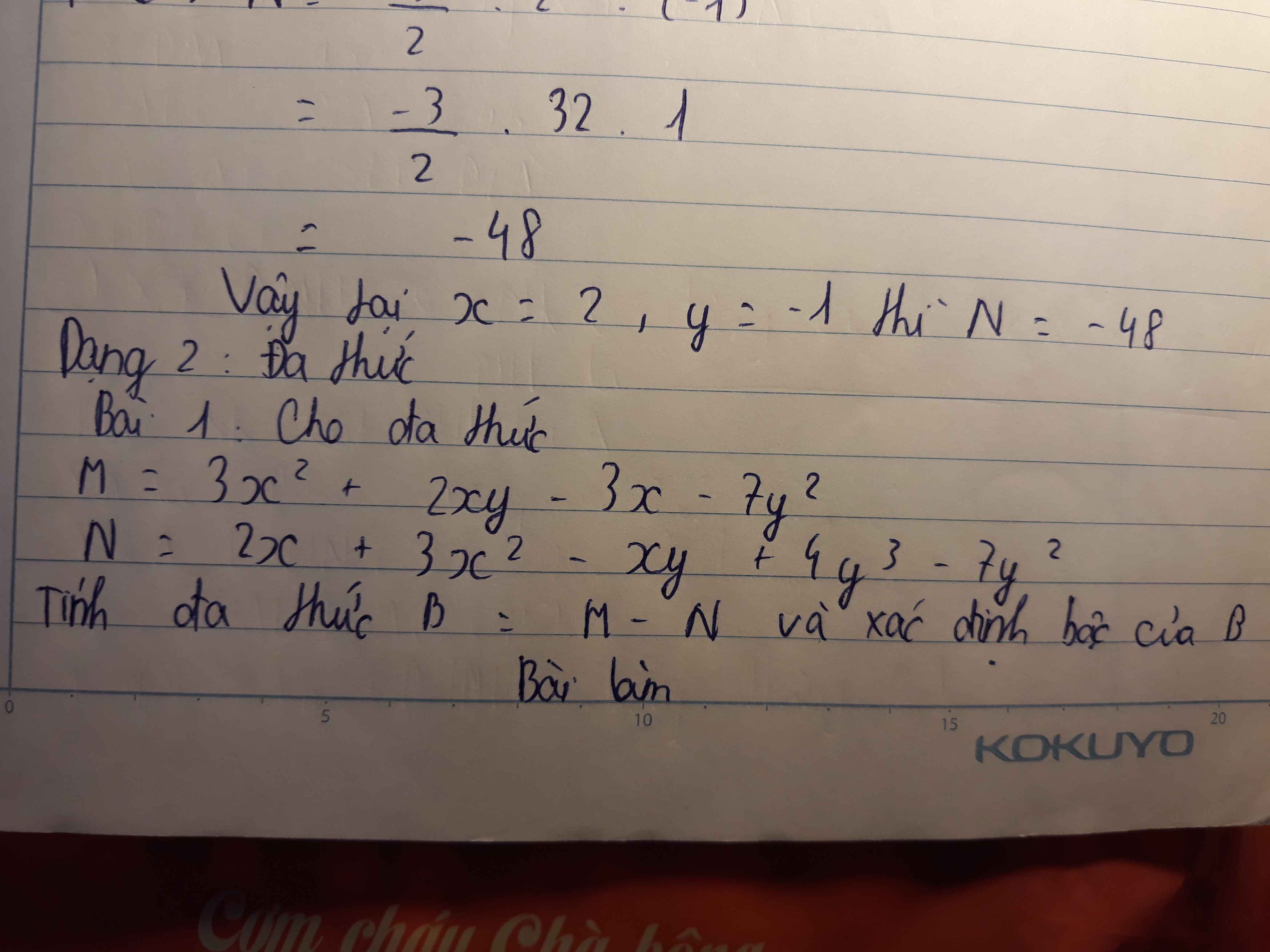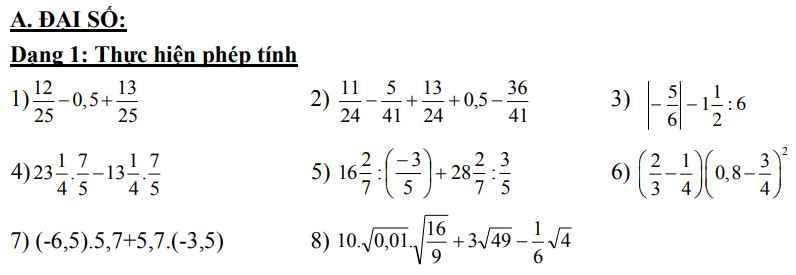a, \(=\dfrac{1}{2}x^4y^3z\)
b, \(=-5x^3y^2-\dfrac{3}{4}x^3y^2+9x^3y^2=\dfrac{-23}{4}x^3y^2+9x^3y^2\)
c, \(=\left(1-\dfrac{1}{2}\right)xy^2-4xy=\dfrac{1}{2}xy^2-4xy\)
d, \(=\dfrac{1}{3}x^3y-\dfrac{3}{8}x^2y^2+\dfrac{2}{5}xy^3\)
a) \(3x^2y.[\dfrac{1}{6}x^2y^2z]\)
=(3.\(\dfrac{1}{6}\)) (\(x^2.x^2\)) . (\(y.\)\(y^2\)) \(z\)
=\(\dfrac{1}{2}\)\(x^4y^3z\)
b) -5\(x^3\)\(y^2\)+10\(x^3y^2\)+(\(\dfrac{-3}{4}\)\(x^3y^2\))-\(x^3y^2\)
= \([\)(-5)+10+\(\dfrac{-3}{4}\)+(-1)\(]\)\(x^3y^2\)
=\(\dfrac{13}{4}\text{}\text{}\)\(x^3y^2\)
c)\(\dfrac{1}{3}x^2y\)+\(xy^2\)-\(xy\)-\(\dfrac{1}{2}\)\(xy^2\)-3\(xy\)-\(\dfrac{1}{3}x^2y\)
=\([\)\(\dfrac{1}{3}x^2y\)+(-\(\dfrac{1}{3}x^2y\))\(]\)+(1\(xy^2\)-\(\dfrac{1}{2}\)\(xy^2\))+\([\)-1\(xy\)+(-3\(xy\))\(]\)
=0+\(\dfrac{1}{2}\)\(xy^2\)+-4\(xy\) (mik tính cái này nhanh)
=\(\dfrac{1}{2}\)\(xy^2\)+-4\(xy\)(mik không chắc kết quả này đúng)
d)\(\dfrac{1}{2}\)\(xy\).(\(\dfrac{2}{3}\)\(x^2\)-\(\dfrac{3}{4}\)\(xy\)+\(\dfrac{4}{5}\)\(y^2\))