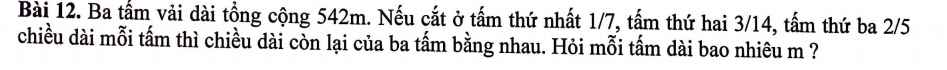Question

Giúp mình với, mình cảm ơn

Answer 1

Lời giải:

Gọi độ dài tấm vải 1,2,3 lần lượt là $a,b,c$. Theo bài ra ta có:

$a+b+c=542(1)$
$\frac{6}{7}a=\frac{11}{14}b=\frac{3}{5}c$

$\Rightarrow b=\frac{12}{11}a; c=\frac{10}{7}a$. Thay vô $(1)$:

$a+\frac{12}{11}a+\frac{10}{7}a=542$

$a(1+\frac{12}{11}+\frac{10}{7})=542$

$a.\frac{271}{77}=542$

$a=154$

$b=\frac{12}{11}a=168$

$c=\frac{10}{7}a=220$

Answer 2

Lời giải:

Gọi độ dài tấm vải 1,2,3 lần lượt là $a,b,c$. Theo bài ra ta có:

$a+b+c=542(1)$
$\frac{6}{7}a=\frac{11}{14}b=\frac{3}{5}c$

$\Rightarrow b=\frac{12}{11}a; c=\frac{10}{7}a$. Thay vô $(1)$:

$a+\frac{12}{11}a+\frac{10}{7}a=542$

$a(1+\frac{12}{11}+\frac{10}{7})=542$

$a.\frac{271}{77}=542$

$a=154$

$b=\frac{12}{11}a=168$

$c=\frac{10}{7}a=220$