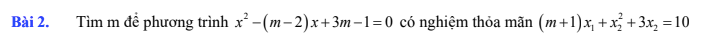Bài 2.
\(x^2-\left(m-2\right)x+3m-1=0\)
\(\Delta=\left(m-2\right)^2-4\left(3m-1\right)=m^2-16m+8\)
PT có hai nghiệm \(x_1,x_2\)\(\Leftrightarrow\Delta\ge0\Leftrightarrow m^2-16m+8\ge0\)
Khi đó, áp dụng hệ thức Vi - et ta có: \(\left\{{}\begin{matrix}x_1+x_2=m-2\\x_1x_2=3m-1\end{matrix}\right.\)
Để \(\left(m+1\right)x_1+x_2^2+3x_2=10\Leftrightarrow\left(m-2\right)x_1+3x_1+x_2^2+3x_2=10\)
\(\Leftrightarrow\left(x_1+x_2\right)x_1+x_2^2+3\left(x_1+x_2\right)=10\)
\(\Leftrightarrow x_1^2+x_2^2+x_1x_2+3\left(x_1+x_2\right)=10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-x_1x_2+3\left(x_1+x_2\right)=10\)
\(\Leftrightarrow\left(m-2\right)^2-\left(3m-1\right)+3\left(m-2\right)=10\)
\(\Leftrightarrow m^2-4m-11=0\Leftrightarrow\left[{}\begin{matrix}m=2+\sqrt{15}\left(L\right)\\m=2-\sqrt{15}\left(TM\right)\end{matrix}\right.\)
Bài 8.
\(x^2-2x+m-3=0\)
\(\Delta=4-4\left(m-3\right)=-4m+16\)
a) Phương trình có 2 nghiệm phân biệt \(\Leftrightarrow\Delta>0\Leftrightarrow-4m+16>0\Leftrightarrow m< 4\)
b) Áp dụng hệ thức Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-3\end{matrix}\right.\)
Để \(x_1^2-2x_2+x_1x_2=16\Leftrightarrow x_1^2-\left(x_1+x_2\right)x_2+x_1x_2=16\)
\(\Leftrightarrow x_1^2-x_2^2=16\) \(\Leftrightarrow\left(x_1+x_2\right)\left(x_1-x_2\right)=16\Leftrightarrow x_1-x_2=8\)
Mà \(x_1+x_2=2\) \(\Rightarrow x_1=5;x_2=-3\Rightarrow x_1x_2=m-3=-15\Rightarrow m=-12\) (TM).