1.
\(x^3-mx^2+\left(m-2\right)x+1=0\)
\(\Leftrightarrow x^3-2x+1-m\left(x^2-x\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x-1\right)-mx\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-\left(m-1\right)x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2-\left(m-1\right)x-1=0\left(1\right)\end{matrix}\right.\)
Để pt có 3 nghiệm pb \(\Leftrightarrow f\left(x\right)=x^2-\left(m-1\right)x-1=0\) có 2 nghiệm pb khác 1
\(\Leftrightarrow f\left(1\right)=1-\left(m-1\right)-1\ne0\) (pt trên hiển nhiên luôn có 2 nghiệm pb trái dấu do \(ac=-1< 0\))
\(\Leftrightarrow m\ne1\)
2.
\(x^3+\left(m+1\right)x^2+2mx+4=0\)
\(\Leftrightarrow x^3+x^2+4+mx\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-x+2\right)+mx\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+\left(m-1\right)x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x^2+\left(m-1\right)x+2=0\left(1\right)\end{matrix}\right.\)
Pt có 2 nghiệm khi:
TH1: (1) có nghiệm kép khác 2
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(m-1\right)^2-8=0\\-\dfrac{b}{2a}=\dfrac{1-m}{2}\ne2\end{matrix}\right.\) \(\Rightarrow m=1\pm2\sqrt{2}\)
TH2: (1) có 2 nghiệm pb và 1 nghiệm trong đó bằng 2
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(m-1\right)^2-8>0\\f\left(2\right)=4+2\left(m-1\right)+2=0\end{matrix}\right.\) \(\Rightarrow m=-2\)

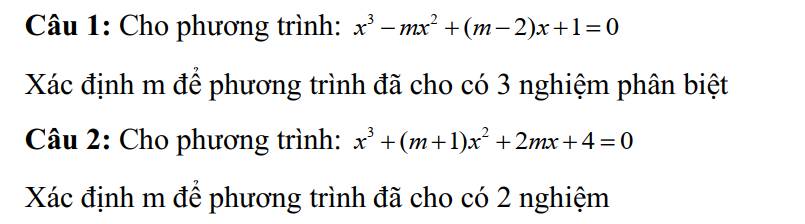 GIÚP MÌNH VỚI! HELP MEEEEEEE 😭
GIÚP MÌNH VỚI! HELP MEEEEEEE 😭















 😭😭😭😭
😭😭😭😭