Câu 1:
$a$ không là số hữu tỉ âm lẫn dương thì $a=0$
$\Leftrightarrow 2x-1=0$
$\Leftrightarrow x=\frac{1}{2}$
Đáp án A.
Câu 2:
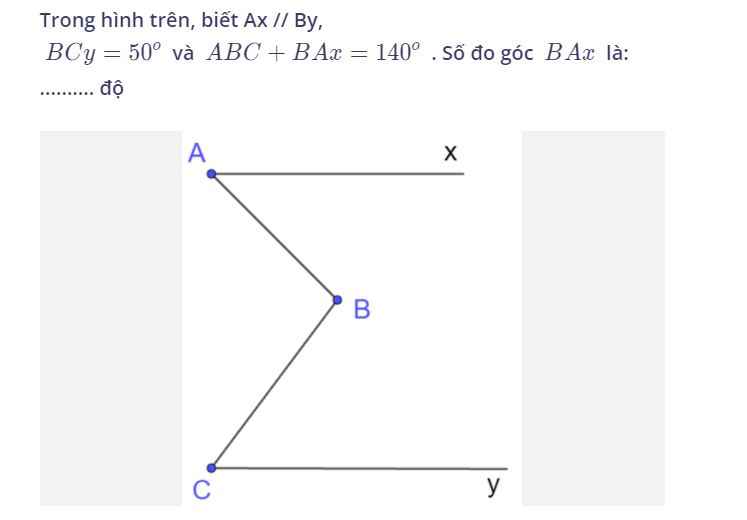
Theo tính chất 2 đường song song thì:
$x=40^0+(180^0-120^0)=100^0$
Đáp án C.
Câu 3:
Áp dụng BĐT dạng $|a|+|b|\geq |a+b|$ ta có:
$A=|x+5|+|x+1|+2021=|x+5|+|-x-1|+2021$
$\geq |x+5-x-1|+2021=4+2021=2025$
Vậy $A_{\min}=2025$
Đáp án A.
Câu 4.
\(A=\frac{2}{6}+\frac{2}{66}+\frac{2}{176}+...+\frac{2}{(5n-4)(5n+1)}\)
\(\frac{5}{2}A=\frac{5}{1.6}+\frac{5}{6.11}+\frac{5}{11.16}+....+\frac{5}{(5n-4)(5n+1)}\)
\(=1-\frac{1}{6}+\frac{1}{6}-\frac{1}{11}+\frac{1}{11}-\frac{1}{16}+....+\frac{1}{5n-4}-\frac{1}{5n+1}\)
\(=1-\frac{1}{5n+1}=\frac{5n}{5n+1}\)
\(\Rightarrow A=\frac{2n}{5n+1}\)
Đáp án D.
Câu 5:
Vì $\triangle ABC=\triangle MNP$ nên $MN=AB=2$ (cm); $MP=AC=3$ (cm)
Chu vi tam giác $MNP$ là:
$MN+MP+NP=2+3+4=9$ (cm)
Đáp án C
Câu 6:
Nửa chu vi thửa ruộng: $100:2=50$ (m)
Chiều dài thửa ruộng: $50:(3+2).3=30$ (m)
Chiều rộng thửa ruộng: $50-30=20$ (m)
Diện tích thửa ruộng: $30.20=600$ (m2)
Đáp án B.
Câu 7:
Vì $O$ là giao 3 đường trung trực nên $OA=OB=OC$
Xét tam giác $ABO$ và $ACO$ có:
$AB=AC$ (do $ABC$ cân tại $A$)
$BO=CO$
$AO$ chung
$\Rightarrow \triangle ABO=\triangle ACO$ (c.c.c)
$\Rightarrow \widehat{ACO}=\widehat{ABO}=30^0$
Đáp án A.
Câu 8:
Qua $E$ kẻ $MN\parallel AB$ và $PQ\parallel AD$ với $M,N,P,Q$ lần lượt thuộc $AD, BC, AB, DC$
Dễ thấy $APEM, PBNE, ENCQ, EMDQ$ là hình chữ nhật. Kết hợp với định lý Pitago ta có:
$EA^2+EC^2=(AM^2+ME^2)+(EQ^2+QC^2)$
$=(BN^2+DQ^2)+(EQ^2+EN^2)$
$=(BN^2+EN^2)+(DQ^2+EQ^2)=EB^2+ED^2$
$\Rightarrow EB^2=EA^2+EC^2-ED^2=3^2+5^2-4^2=18$
$\Rightarrow EB=3\sqrt{2}$ (cm)
Đáp án D.
Câu 9:
Để trọng tâm trùng với trực tâm thì tam giác $ABC$ là tam giác đều.
Mà $ABC$ đã cân tại $B$ rồi nên bất cứ 1 trong 3 góc $\widehat{A}, \widehat{B}, \widehat{C}=60^0$ đều giúp $ABC$ đều.
Đáp án C.
Câu 10:
Vì $ABC$ đều nên trọng tâm $G$ đồng thời là trực tâm $G$.
Do $G$ là trọng tâm nên $GM=\frac{1}{3}AM=1$ (cm)
$BM=\frac{1}{2}BC=\frac{1}{2}AB$
Áp dụng định lý Pitago cho tam giác $ABM$ vuông:
$AB^2-BM^2=AM^2$
$AB^2-(\frac{1}{2}AB)^2=3^2$
$\frac{3}{4}AB^2=3^2$
$AB=2\sqrt{3}$ (cm)
$BM=\frac{1}{2}AB=\sqrt{3}$ (cm)
$GB=\sqrt{BM^2+GM^2}=\sqrt{(\sqrt{3})^2+1^2}=2$ (cm)
Đáp án B.