B\(\dfrac{5}{3}.\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+...+\dfrac{1}{25}-\dfrac{1}{28}\right)\)ài 1:
S1 : \(\dfrac{5}{1.4}+\dfrac{5}{4.7}+...+\dfrac{5}{97.100}\)
= \(\dfrac{5}{3}.\left(\dfrac{1}{1.4}+\dfrac{1}{4.7}+...+\dfrac{1}{97.100}\right)\)
= \(\dfrac{5}{3}.\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\)
= \(\dfrac{5}{3}.\left(1-\dfrac{1}{100}\right)\)
\(=\dfrac{5}{3}.\left(\dfrac{100}{100}-\dfrac{1}{100}\right)\)
= \(\dfrac{5}{3}.\dfrac{99}{100}\)
= \(\dfrac{33}{20}\)
S3 : \(\dfrac{10}{56}+\dfrac{10}{140}+\dfrac{10}{260}+...+\dfrac{10}{1400}\)
= \(\dfrac{5}{28}+\dfrac{5}{70}+\dfrac{5}{130}+...+\dfrac{5}{700}\)
= \(\dfrac{5}{4.7}+\dfrac{5}{7.10}+\dfrac{5}{10.13}+...+\dfrac{5}{25.28}\)
= \(\dfrac{5}{3}.\left(\dfrac{1}{4.7}+\dfrac{1}{7.10}+\dfrac{1}{10.13}+...+\dfrac{1}{25.28}\right)\)
= \(\dfrac{5}{3}.\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+...+\dfrac{1}{25}-\dfrac{1}{28}\right)\)
=\(\dfrac{5}{3}.\left(\dfrac{1}{4}-\dfrac{1}{28}\right)\)
= \(\dfrac{5}{3}.\left(\dfrac{7}{28}-\dfrac{1}{28}\right)\)
= \(\dfrac{5}{3}.\dfrac{6}{28}\)
= \(\dfrac{5}{3}.\dfrac{3}{14}\)
= \(\dfrac{5}{14}\)
S2 : \(\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{2499}\)
=\(\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{49.51}\)
= \(\dfrac{1}{2}.\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{49}-\dfrac{1}{51}\right)\)
= \(\dfrac{1}{2}.\left(\dfrac{1}{3}-\dfrac{1}{51}\right)\)
= \(\dfrac{1}{2}.\dfrac{16}{51}\)
= \(\dfrac{8}{51}\)
S4 : \(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{300}}\)
3S = \(\dfrac{3}{3}+\dfrac{3}{3^2}+\dfrac{3}{3^3}+\dfrac{3}{3^4}+...+\dfrac{3}{3^{300}}\)
3S = \(1+\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{299}}\)
3S-S = \(\left(1+\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{299}}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{300}}\right)\)
2S = \(1+\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{299}}-\dfrac{1}{3}-\dfrac{1}{3^2}-\dfrac{1}{3^3}-\dfrac{1}{3^4}-...-\dfrac{1}{3^{300}}\)
2S = \(1-\dfrac{1}{3^{300}}\)
Đúng 3
Bình luận (1)
Các câu hỏi tương tự
Giúp mình bài này với ạ! Giải chi tiết giúp mình nhé! Mình cảm ơn ạ!

Giúp mình bài này với ạ! Giải chi tiết giúp mình nhé! Mình cảm ơn ạ!
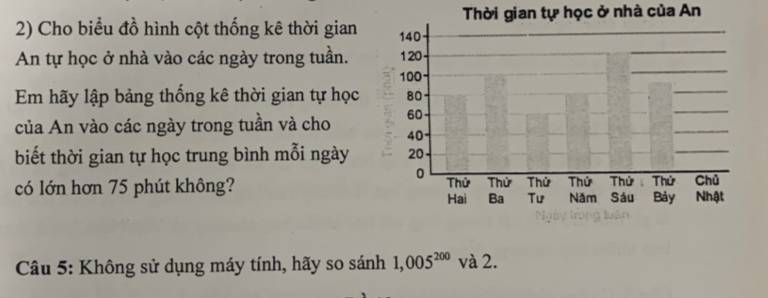
Giúp mình bài này với ạ! Giải chi tiết giúp mình nhé! Mình cảm ơn ạ!
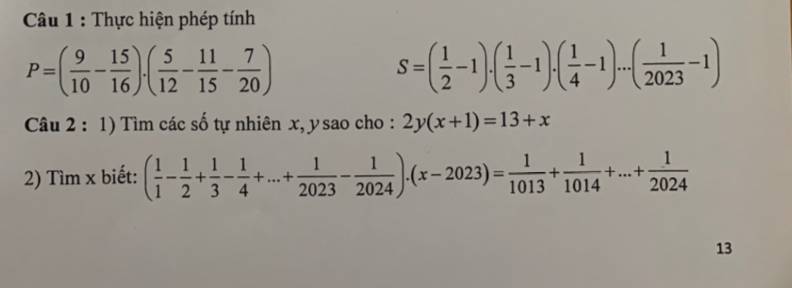
Giúp mình bài này với ạ! Giải chi tiết giúp mình nhé! Mình cảm ơn ạ!

Giúp mình bài này với ạ! Giải chi tiết giúp mình nhé! Mình cảm ơn ạ!
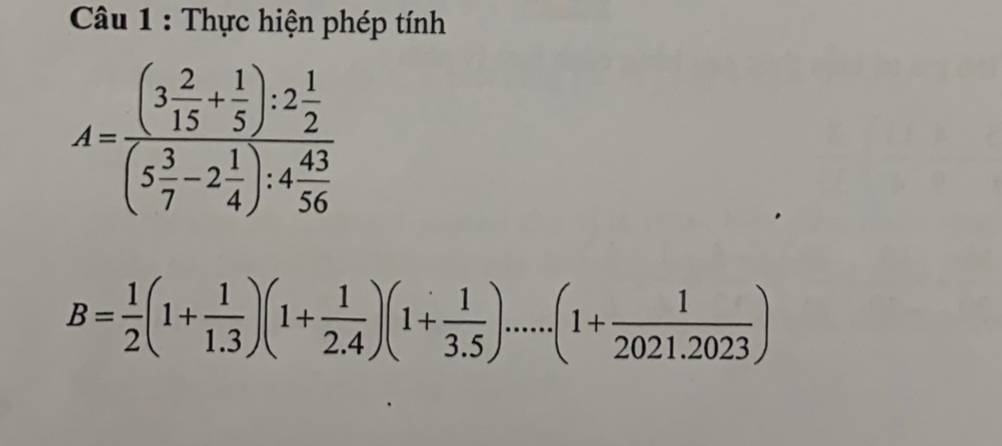
giúp mình với ạ mình cần cách làm rõ ràng ạ cảm ơn ạ!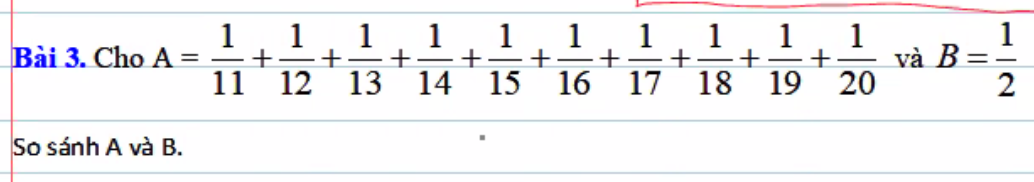
Ai giúp mình với ạ mình cảm ơn trước ạ
Các bn ơi cho tui hỏi với dc ko ạ bài bài 2
D 23. 17 - 23.14 với ạ mình chưa bt bài này ạ giúp mình với ạ
CTR: 1/2+1/3+1/4+...+1/100
GIÚP MÌNH VỚI Ạ. MÌNH CẦM GẤP. CẢM ƠN MỌI NGƯỜI!
Cô THương Hoài giúp em với ạ













