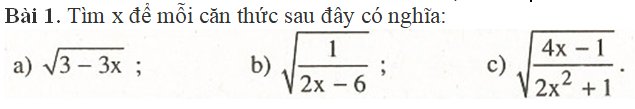Question

      giúp mình với ạ   

Answer 1

\(a,\sqrt{3-3x}\) có nghĩa \(\Leftrightarrow3-3x\ge0\Leftrightarrow-3x\ge-3\Leftrightarrow x\le1\)

\(b,\sqrt{\dfrac{1}{2x-6}}\) có nghĩa \(\Leftrightarrow2x-6>0\Leftrightarrow2x>6\Leftrightarrow x>3\)

\(c,\sqrt{\dfrac{4x-1}{2x^2+1}}\) có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}4x-1\ge0\\2x^2+1>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}4x\ge1\\2x^2>-1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{4}\\x^2>-\dfrac{1}{2}\left(LD\forall x\right)\end{matrix}\right.\)

\(\Leftrightarrow x\ge\dfrac{1}{4}\)