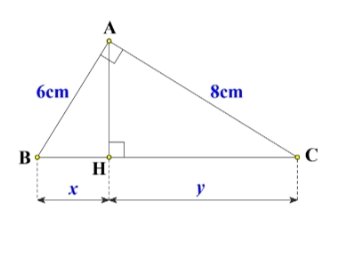
Ta có: \(\Delta ABC\) vuông tại A và đường cao AH
Áp dụng đính lý Py-ta-go ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu ta có:
\(AB^2=BC\cdot BH\Rightarrow BH=x=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
\(AC^2=BC\cdot CH\Rightarrow CH=y=\dfrac{AC^2}{BC}=\dfrac{8^2}{10}=6,4\left(cm\right)\)
Áp dụng định lí pitago trong \(\Delta ABC\) vuông tại A:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=10cm\)
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại A:
\(\left\{{}\begin{matrix}AB^2=BH.BC\\AC^2=CH.BC\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6cm\\CH=\dfrac{AC^2}{BC}=\dfrac{8^2}{10}=6,4cm\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=3,6cm\\y=6,4cm\end{matrix}\right.\)
Giúp mình với ạ, mình cần gấp lắm ạ!
