\(a,2\left|3x-1\right|+1=5\\ \Rightarrow2\left|3x-1\right|=5-1\\ \Rightarrow2\left|3x-1\right|=4\\ \Rightarrow\left|3x-1\right|=4:2\\ \Rightarrow\left|3x-1\right|=2\\ \Rightarrow\left[{}\begin{matrix}3x-1=2\\3x-1=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}3x=3\\3x=-1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)
\(b,\left|\dfrac{x}{2}-1\right|=3\\ \Rightarrow\left[{}\begin{matrix}\dfrac{x}{2}-1=3\\\dfrac{x}{2}-1=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\dfrac{x}{2}=4\\\dfrac{x}{2}=-2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=8\\x=-4\end{matrix}\right.\)
\(c,\left|-x+\dfrac{2}{5}\right|+\dfrac{1}{2}=3,5\\ \Rightarrow\left|-x+\dfrac{2}{5}\right|=3,5-\dfrac{1}{2}\\ \Rightarrow\left|-x+\dfrac{2}{5}\right|=3\\ \Rightarrow\left[{}\begin{matrix}-x+\dfrac{2}{5}=3\\-x+\dfrac{2}{5}=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}-x=\dfrac{13}{5}\\-x=-\dfrac{17}{5}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{13}{5}\\x=\dfrac{17}{5}\end{matrix}\right.\)
\(d,\left|x-\dfrac{1}{3}\right|=2\dfrac{3}{5}\\ \Rightarrow\left|x-\dfrac{1}{3}\right|=\dfrac{13}{5}\\ \Rightarrow\left[{}\begin{matrix}x-\dfrac{1}{3}=\dfrac{13}{5}\\x-\dfrac{1}{3}=-\dfrac{13}{5}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{13}{5}+\dfrac{1}{3}\\x=-\dfrac{13}{5}+\dfrac{1}{3}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\dfrac{44}{15}\\x=-\dfrac{34}{15}\end{matrix}\right.\)











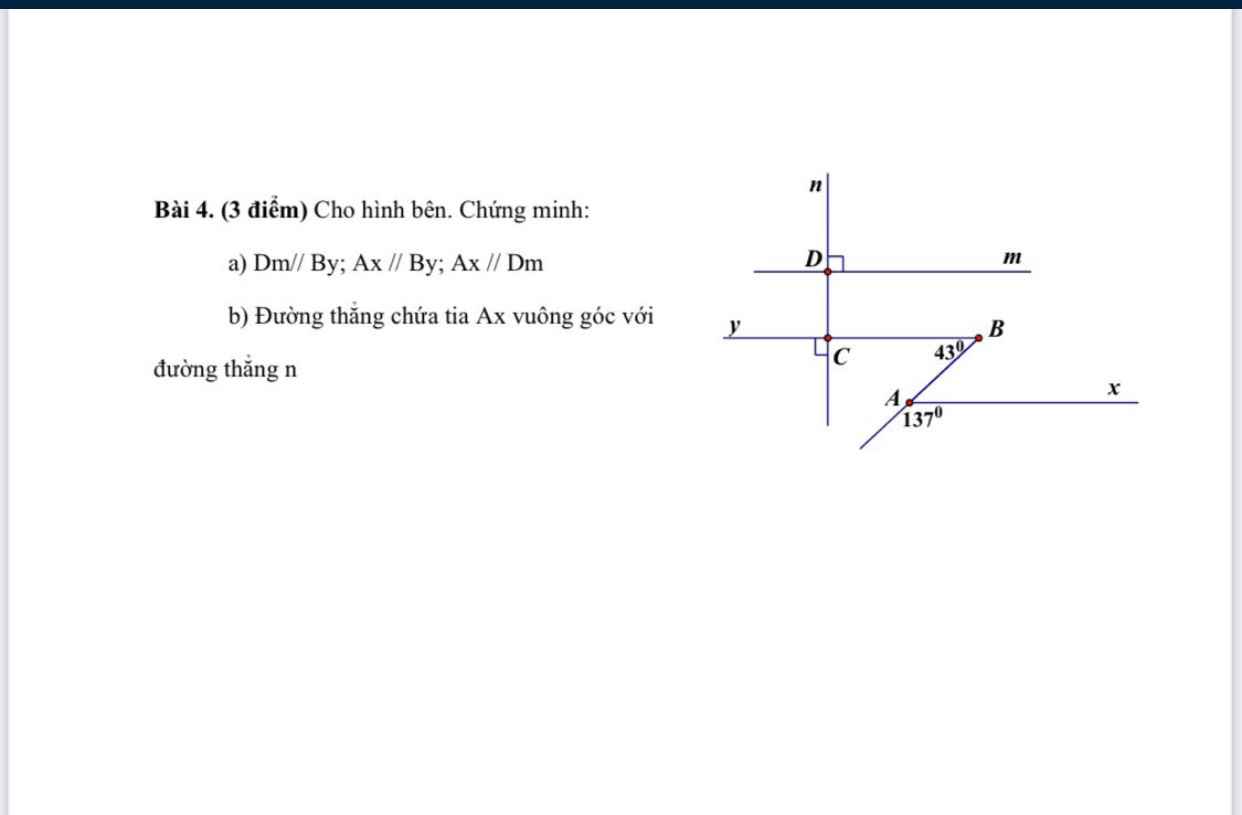





 Giúp mình với ạ, mình đang cần gấp
Giúp mình với ạ, mình đang cần gấp 

