Giúp mình với ạ mình cần gấp

Bài 1 (3,0 điểm) Cho tam giác \( ABC \) nhọn, đường cao \( DB, CE \) cắt nhau ở \( H \), \( AH \) cắt \( BC \) tại \( M \).
a) Chứng minh rằng: \( AM \perp BC \) và \(\widehat{BAM} = \widehat{ECB}\).
b) Lấy điểm \( K \) sao cho \( AB \) là trung trực của \( HK \). Chứng minh rằng: \(\widehat{KAB} = \widehat{KCB}\).
Bài 2 (3,0 điểm) Cho tam giác \( ABC \) vuông ở \( A \) có \(\widehat{ACB} = 30^\circ\), đường cao \( AH \). Trên đoạn \( HC \) lấy điểm \( D \) sao cho \( HD = HB \). Từ \( C \) kẻ \( CE \) vuông góc với \( AD \). Chứng minh:
a) Tam giác \( ABD \) đều và tam giác \( ADC \) cân.
b) \( AH = CE \).
c) \( EH \parallel AC \).
Bài 3 (4,0 điểm) Cho \( \triangle ABC \) cân tại \( A \), kẻ \( AH \) vuông góc với \( BC \) (\( H \in BC \)).
a) Chứng minh \( HB = HC \) và \( AH \) là tia phân giác của \( \widehat{BAC} \).
b) Lấy \( D \) trên tia đối của tia \( BC \) sao cho \( BD = BH \), lấy \( E \) trên tia đối của tia \( BA \) sao cho \( BE = BA \). Chứng minh rằng: \( DE \parallel AH \).
c) So sánh \(\widehat{DAB}\) và \(\widehat{BAH}\).
d) Lấy điểm \( F \) sao cho \( D \) là trung điểm của \( EF \). Gọi \( G \) là trung điểm của \( EC \). Chứng minh rằng: \( F, B, G \) thẳng hàng.
Bài 1:
a: Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại M
b: H đối xứng K qua AB
=>AB là đường trung trực của HK
=>AB\(\perp\)HK
mà AB\(\perp\)HE tại E
nên E là trung điểm của HK và AB\(\perp\)KH tại E
Xét ΔAEH vuông tại E và ΔAEK vuông tại E có
AE chung
EH=EK
Do đó: ΔAEH=ΔAEK
=>\(\widehat{EAH}=\widehat{EAK}\)
mà \(\widehat{EAH}=\widehat{KCB}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{KAB}=\widehat{KCB}\)
Bài 2:
a: Xét ΔAHB vuông tại H và ΔAHD vuông tại H có
AH chung
HB=HD
Do đó: ΔAHB=ΔAHD
=>AB=AD
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-30^0=60^0\)
Xét ΔABD có AB=AD và \(\widehat{ABD}=60^0\)
nên ΔABD đều
Ta có: \(\widehat{DAC}+\widehat{DAB}=\widehat{BAC}=90^0\)
\(\widehat{DCA}+\widehat{DBA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{DAB}=\widehat{DBA}\)(ΔABD đều)
nên \(\widehat{DAC}=\widehat{DCA}\)
=>ΔDAC cân tại D
b: Xét ΔDHA vuông tại H và ΔDEC vuông tại E có
DA=DC
\(\widehat{ADH}=\widehat{CDE}\)(hai góc đối đỉnh)
Do đó: ΔDHA=ΔDEC
=>AH=CE
c: ΔDHA=ΔDEC
=>DH=DE
Xét ΔDAC và ΔDEH có
\(\dfrac{DE}{DA}=\dfrac{DH}{DC}\)
\(\widehat{ADC}=\widehat{EDH}\)
Do đó: ΔDAC~ΔDEH
=>\(\widehat{DAC}=\widehat{DEH}\)
mà hai góc này là hai góc ở vị trí so le trong
nên EH//AC







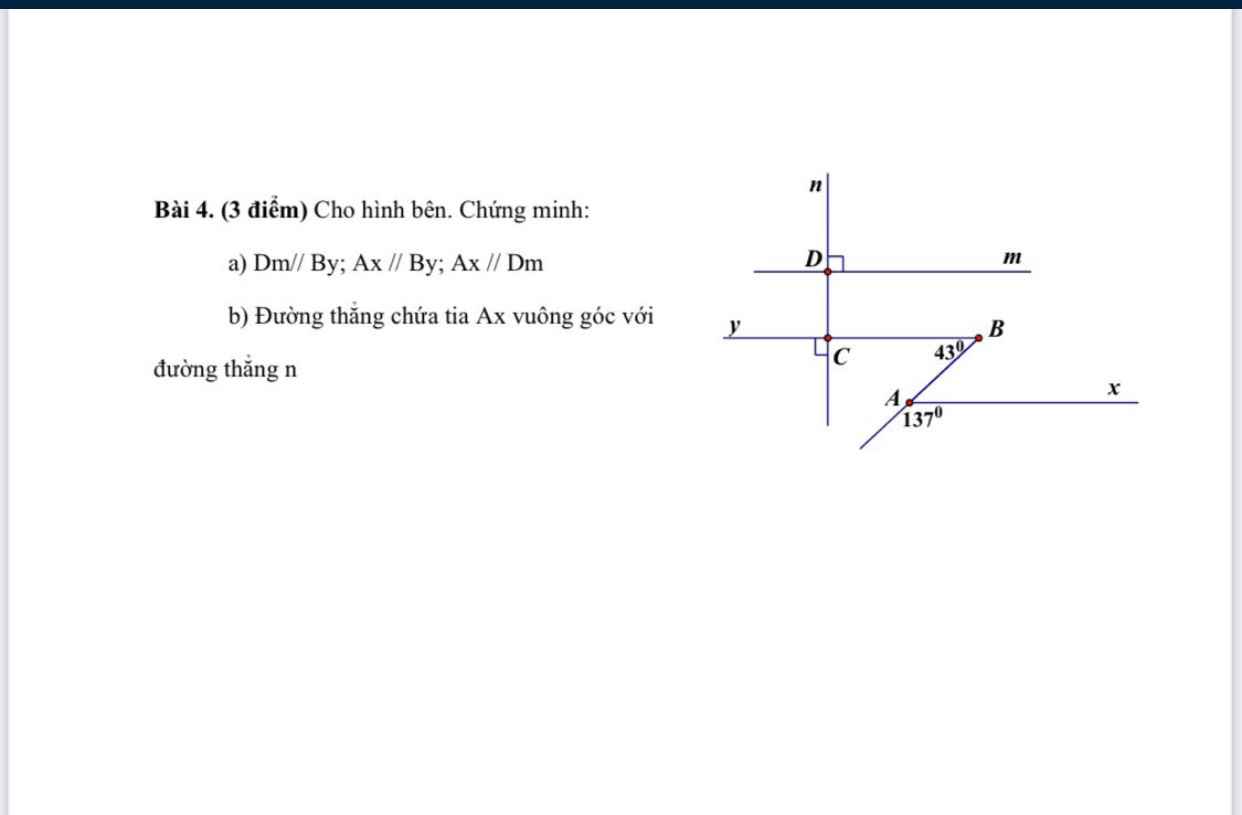














 Giúp mình với ạ, mình đang cần gấp
Giúp mình với ạ, mình đang cần gấp