Các câu hỏi tương tự
Xét các khẳng định sau i) Nếu hàm số yf(x) có đạo hàm cấp hai trên R và đạt cực tiểu tại
x
x
0
thì
f
x
0
0
f...
Đọc tiếp
Xét các khẳng định sau
i) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực tiểu tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 > 0
ii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và đạt cực đại tại x = x 0 thì f ' x 0 = 0 f ' ' x 0 < 0
iii) Nếu hàm số y=f(x) có đạo hàm cấp hai trên R và f ' ' x 0 = 0 thì hàm số không đạt cực trị tại x = x 0
Số khẳng định đúng trong các khẳng định trên là
A. 0
B. 1
C. 2
D. 3
Cho hàm số
y
1
x
.Đạo hàm cấp hai của hàm số là:
Đọc tiếp
Cho hàm số y = 1 x .Đạo hàm cấp hai của hàm số là:
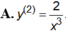
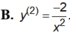
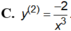
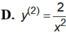
Giả sử hàm số f có đạo hàm cấp n trên R thỏa mãn
f
1
-
x
+
x
2
f
x
2
x
với mọi
x
∈
R
. Tính tích phân
I
∫
0
1
xf...
Đọc tiếp
Giả sử hàm số f có đạo hàm cấp n trên R thỏa mãn f 1 - x + x 2 f ' ' x = 2 x với mọi x ∈ R . Tính tích phân I = ∫ 0 1 xf ' x dx .
A. I = 1
B. I = 2
C. I = 1/3
D. I = 2/3
Đạo hàm cấp 5 của hàm số y x ln x là A. B. C. D.
Đọc tiếp
Đạo hàm cấp 5 của hàm số y =x ln x là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số
y
1
x
. Khi đó
y
n
x
bằng (đạo hàm cấp n của hàm số) A.
y
n
x
−
1
n
n
!
x
n...
Đọc tiếp
Cho hàm số y = 1 x . Khi đó y n x bằng (đạo hàm cấp n của hàm số)
A. y n x = − 1 n n ! x n + 1
B. y n x = n ! x n + 1
C. y n x = − 1 n n ! x n
D. y n x = n ! x n
Cho hàm số
f
(
x
)
x
2
1
-
x
. Đạo hàm cấp 2018 của hàm số f(x) là:
Đọc tiếp
Cho hàm số f ( x ) = x 2 1 - x . Đạo hàm cấp 2018 của hàm số f(x) là:
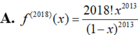
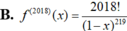
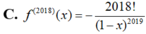
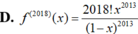
Cho hàm số
y
4
(
sin
4
x
+
cos
4
x
)
-
3
tan
...
Đọc tiếp
Cho hàm số y = 4 ( sin 4 x + cos 4 x ) - 3 tan 2 x + cot 2 x
Tính đạo hàm cấp hai y’’?
![]()
![]()
![]()
![]()
Câu hỏi xét tính đơn điệu của hàm số
Giúp mình với mình cần gấp ạ
Cho hàm số yf(x) có đạo hàm cấp 2 trên khoảng K và . Mệnh đề nào sau đây đúng? A. Nếu thì là điểm cực trị của hàm số B. Nếu thì là điểm cực trị của hàm số thì C. Nếu thì là điểm cực trị của hàm số thì D. Nếu thì là điểm cực trị của hàm số thì
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm cấp 2 trên khoảng K và ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
A. Nếu ![]() thì
thì ![]() là điểm cực trị của hàm số
là điểm cực trị của hàm số ![]()
B. Nếu ![]() thì là điểm cực trị của hàm số
thì là điểm cực trị của hàm số ![]() thì
thì ![]()
C. Nếu ![]() thì là điểm cực trị của hàm số
thì là điểm cực trị của hàm số ![]() thì
thì ![]()
D. Nếu ![]() thì là điểm cực trị của hàm số
thì là điểm cực trị của hàm số ![]() thì
thì ![]()




