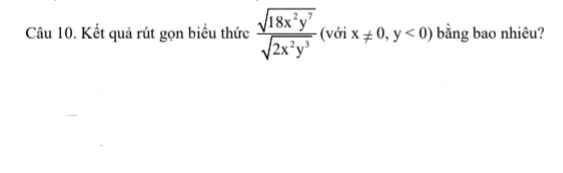giúp mình nhé các bạn
b) Ta có: \(P=\sqrt{\dfrac{14+3\sqrt{3}}{2}}+\sqrt{\dfrac{16+2\sqrt{15}}{3}}-\dfrac{11\sqrt{3}}{6}\)
\(=\sqrt{\dfrac{28+6\sqrt{3}}{2}}+\dfrac{\sqrt{15}+1}{\sqrt{3}}-\dfrac{11\sqrt{3}}{6}\)
\(=\dfrac{3\sqrt{3}+1}{\sqrt{2}}+\dfrac{\sqrt{15}+1}{\sqrt{3}}-\dfrac{11\sqrt{3}}{6}\)
\(=\dfrac{3\sqrt{6}+\sqrt{2}}{2}+\dfrac{3\sqrt{5}+\sqrt{3}}{3}-\dfrac{11\sqrt{3}}{6}\)
\(=\dfrac{3\left(3\sqrt{6}+\sqrt{2}\right)+2\left(3\sqrt{5}+\sqrt{3}\right)-11\sqrt{3}}{6}\)
\(=\dfrac{9\sqrt{6}+3\sqrt{2}+6\sqrt{5}+2\sqrt{3}-11\sqrt{3}}{6}\)
\(=\dfrac{9\sqrt{6}+3\sqrt{2}+6\sqrt{5}-9\sqrt{3}}{6}\)
\(=\dfrac{3\sqrt{6}+\sqrt{2}+2\sqrt{5}-3\sqrt{3}}{2}\)
c) Ta có: \(a+b=\sqrt{28+6\sqrt{3}}-\sqrt{31-12\sqrt{3}}\)
\(=3\sqrt{3}+1-3\sqrt{3}+2\)
=3
Ta có: \(P=a^2+b^2+2ab+4a+4b\)
\(=\left(a+b\right)^2+4\left(a+b\right)\)
\(=\left(a+b\right)\left(a+b+4\right)\)
\(=3\cdot7=21\)
