a)
\(\left(3x+2\right)\left(x^2-1\right)=\left(9x^2-4\right)\left(x+1\right)\\ \Leftrightarrow\left(3x+2\right)\left(x-1\right)\left(x+1\right)-\left(3x-2\right)\left(3x+2\right)\left(x+1\right)=0\\ \Leftrightarrow\left(3x+2\right)\left(x+1\right)\left(x-1-3x+2\right)=0\\ \Leftrightarrow\left(3x+2\right)\left(x+1\right)\left(1-2x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=-1\\x=\dfrac{1}{2}\end{matrix}\right.\)
b)
\(x\left(x+3\right)\left(x-3\right)-\left(x+2\right)\left(x^2-2x+4\right)=0\\ \Leftrightarrow x\left(x^2-9\right)-\left(x^3+2^3\right)=0\\ \Leftrightarrow x^3-9x-x^3-8=0\\ \Leftrightarrow-9x-8=0\\ \Leftrightarrow x=-\dfrac{8}{9}\)
c)
\(2x\left(x-3\right)+5\left(x-3\right)=0\\ \Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)
d)
\(\left(3x-1\right)\left(x^2+2\right)=\left(3x-1\right)\left(7x-10\right)\\ \Leftrightarrow\left(3x-1\right)\left(x^2+2\right)-\left(3x-1\right)\left(7x-10\right)=0\\ \Leftrightarrow\left(3x-1\right)\left(x^2+2-7x+10\right)=0\\ \Leftrightarrow\left(3x-1\right)\left(x^2-7x+12\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x-1=0\\x^2-7x+12=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=4\\x=3\end{matrix}\right.\)
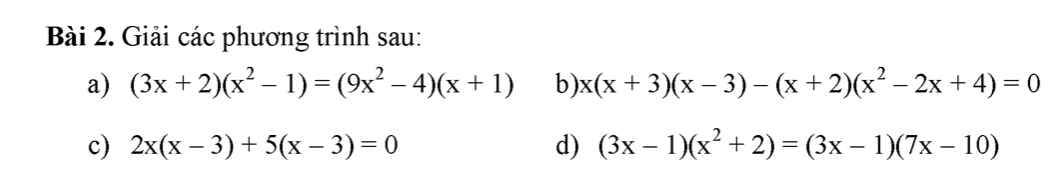
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
