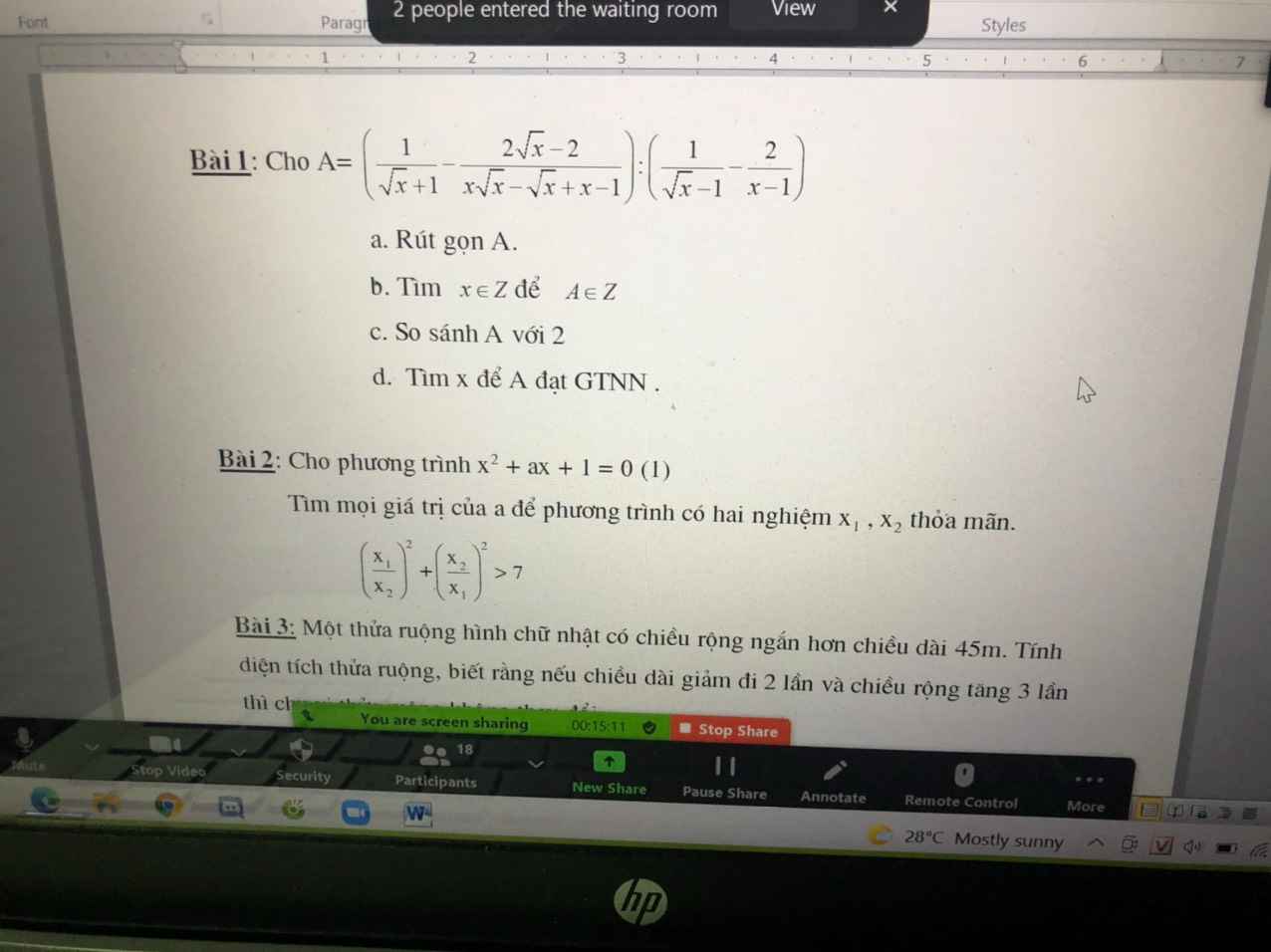
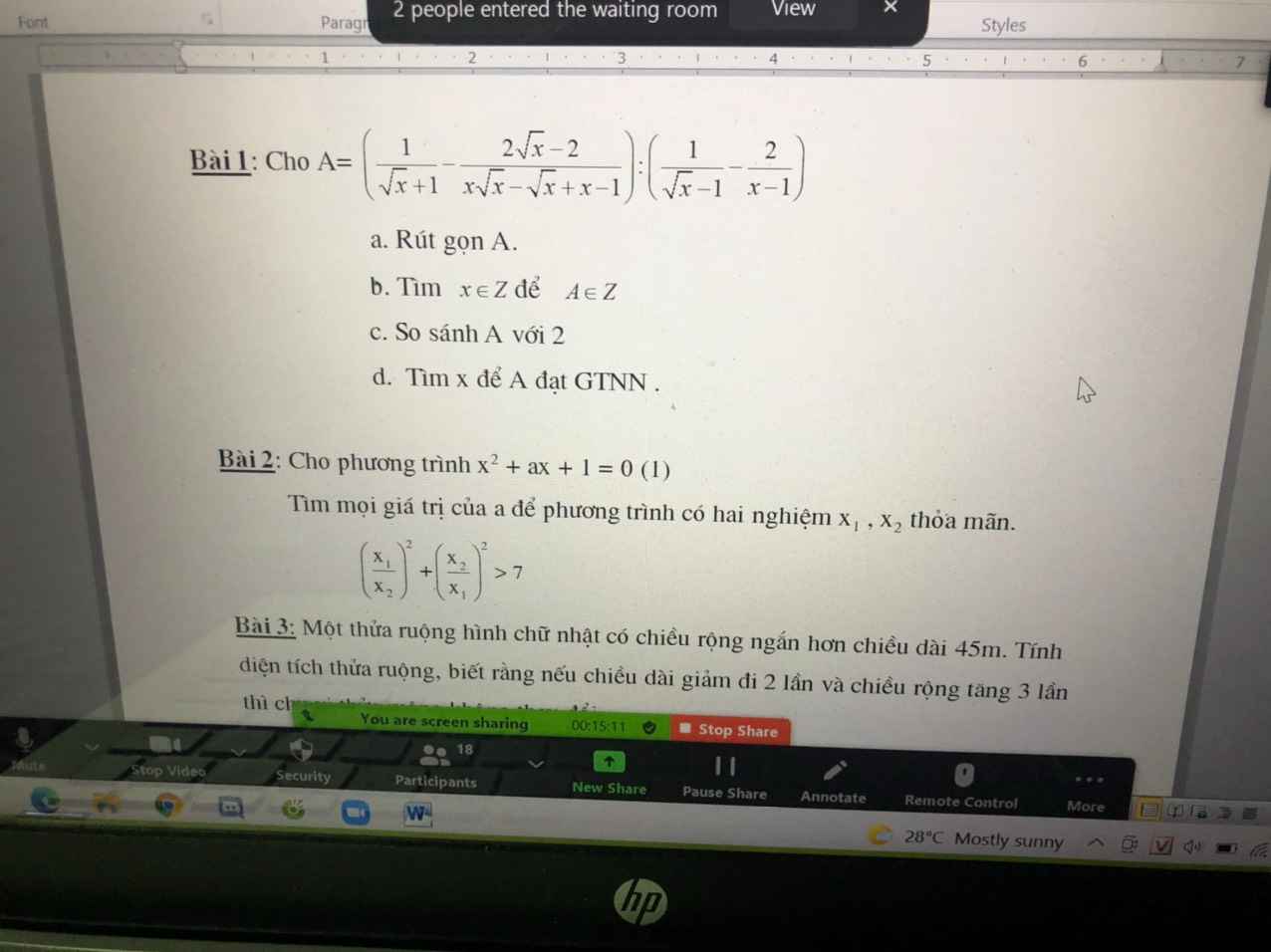
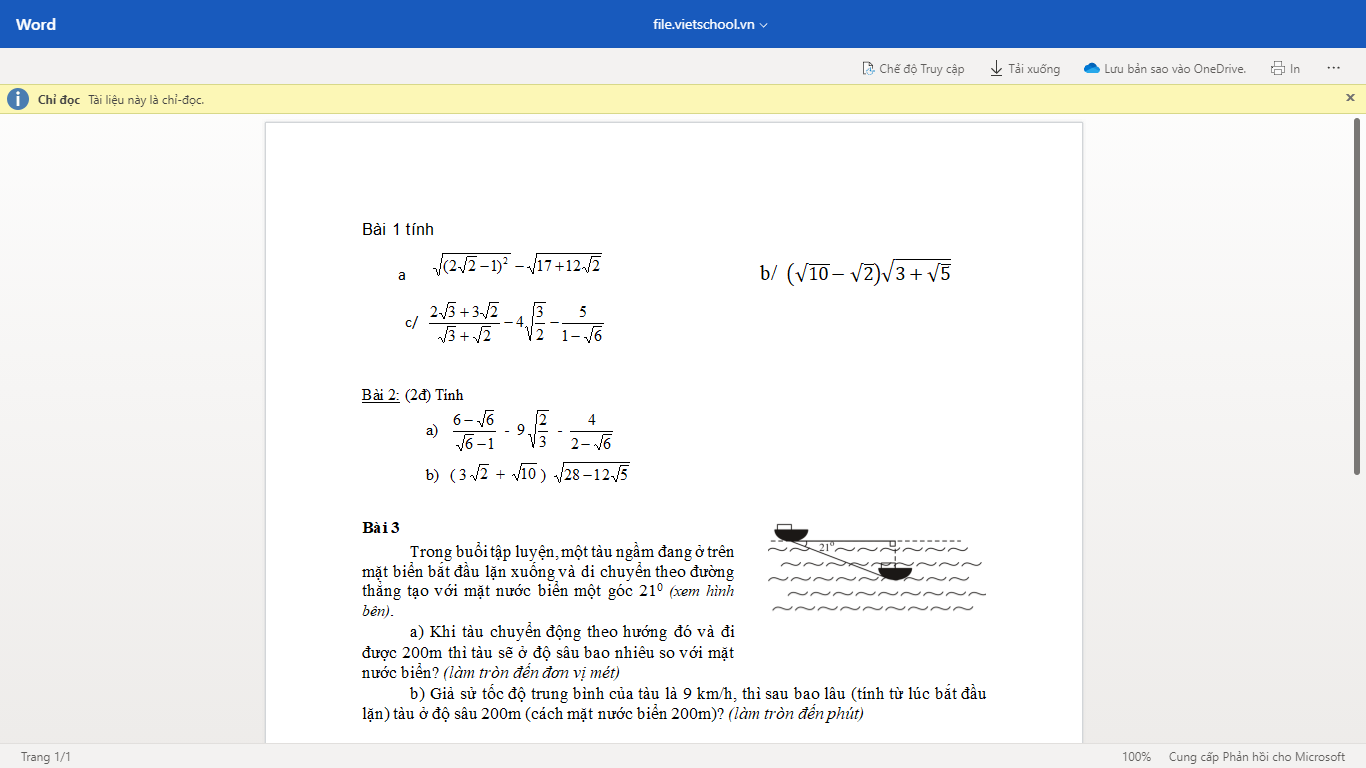
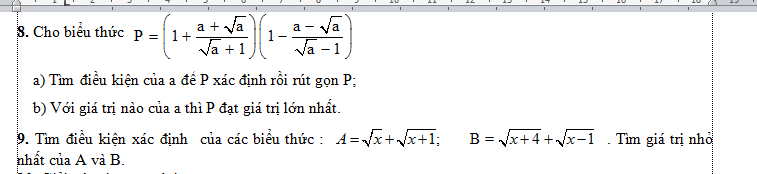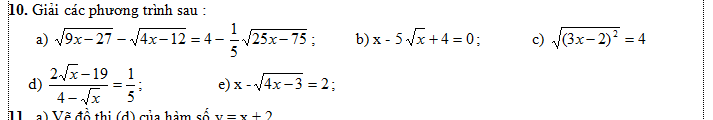A=\(\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{2\sqrt{x}-2}{x\sqrt{x}-\sqrt{x}+x-1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2}{x-1}\right)\) (đk: \(x\ge0;x\ne1\))
\(=\left[\dfrac{1}{\sqrt{x}+1}-\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(x-1\right)}\right]:\dfrac{\sqrt{x}+1-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\left[\dfrac{1}{\sqrt{x}+1}-\dfrac{2}{\left(\sqrt{x}+1\right)^2}\right]:\dfrac{1}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+1-2}{\left(\sqrt{x}+1\right)^2}.\left(\sqrt{x}+1\right)=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
b, \(A=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}=1-\dfrac{2}{\sqrt{x}+1}\)
Để \(A\in Z\Leftrightarrow\dfrac{2}{\sqrt{x}+1}\in Z\) mà với mọi \(x\in Z\),\(x\ge0\) thì \(\left\{{}\begin{matrix}\dfrac{2}{\sqrt{x}+1}>0\\\dfrac{2}{\sqrt{x}+1}\le\dfrac{2}{\sqrt{0}+1}=2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{2}{\sqrt{x}+1}=1\\\dfrac{2}{\sqrt{x}+1}=2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(L\right)\\x=0\left(TM\right)\end{matrix}\right.\)
Vậy x=0 thì A=-1
c, Vì \(\dfrac{2}{\sqrt{x}+1}>0\Rightarrow\) \(A=1-\dfrac{2}{\sqrt{x}+1}< 1< 2\)
Vậy A<2
d, \(\sqrt{x}\ge0\Rightarrow\sqrt{x}+1\ge1\Leftrightarrow\dfrac{2}{\sqrt{x}+1}\le2\)
\(\Rightarrow1-\dfrac{2}{\sqrt{x}+1}\ge1-2\)
Hay \(A\ge-1\)
Dấu = xảy ra khi x=0