Bài 8:
a: \(x^3-6x^2+11x-6=0\)
=>\(x^3-x^2-5x^2+5x+6x-6=0\)
=>\(x^2\left(x-1\right)-5x\left(x-1\right)+6\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(x^2-5x+6\right)=0\)
=>(x-1)(x-2)(x-3)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=3\end{matrix}\right.\)
b: \(x^3-x^2+3x-10=0\)
=>\(x^3-2x^2+x^2-2x+5x-10=0\)
=>\(x^2\left(x-2\right)+x\left(x-2\right)+5\left(x-2\right)=0\)
=>\(\left(x-2\right)\cdot\left(x^2+x+5\right)=0\)
mà \(x^2+x+5=\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}>=\dfrac{19}{4}\forall x\)
nên x-2=0
=>x=2
c: \(\left(2x^2-3\right)^2-16\left(x+3\right)^2=0\)
=>\(\left(2x^2-3\right)^2-\left(4x+12\right)^2=0\)
=>\(\left(2x^2-3-4x-12\right)\left(2x^2-3+4x+12\right)=0\)
=>\(\left(2x^2-4x-15\right)\left(2x^2+4x+9\right)=0\)
mà \(2x^2+4x+9=2x^2+4x+2+7=2\left(x+1\right)^2+7>=7>0\forall x\)
nên \(2x^2-4x-15=0\)
=>\(x=\dfrac{2\pm\sqrt{34}}{2}\)
d: \(\left(3x^2-7x+2\right)\left(4x^2-3x-1\right)=0\)
=>\(\left[{}\begin{matrix}3x^2-7x+2=0\\4x^2-3x-1=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\left(x-2\right)\left(3x-1\right)=0\\\left(x-1\right)\left(4x+1\right)=0\end{matrix}\right.\)
=>\(x\in\left\{2;\dfrac{1}{3};1;-\dfrac{1}{4}\right\}\)
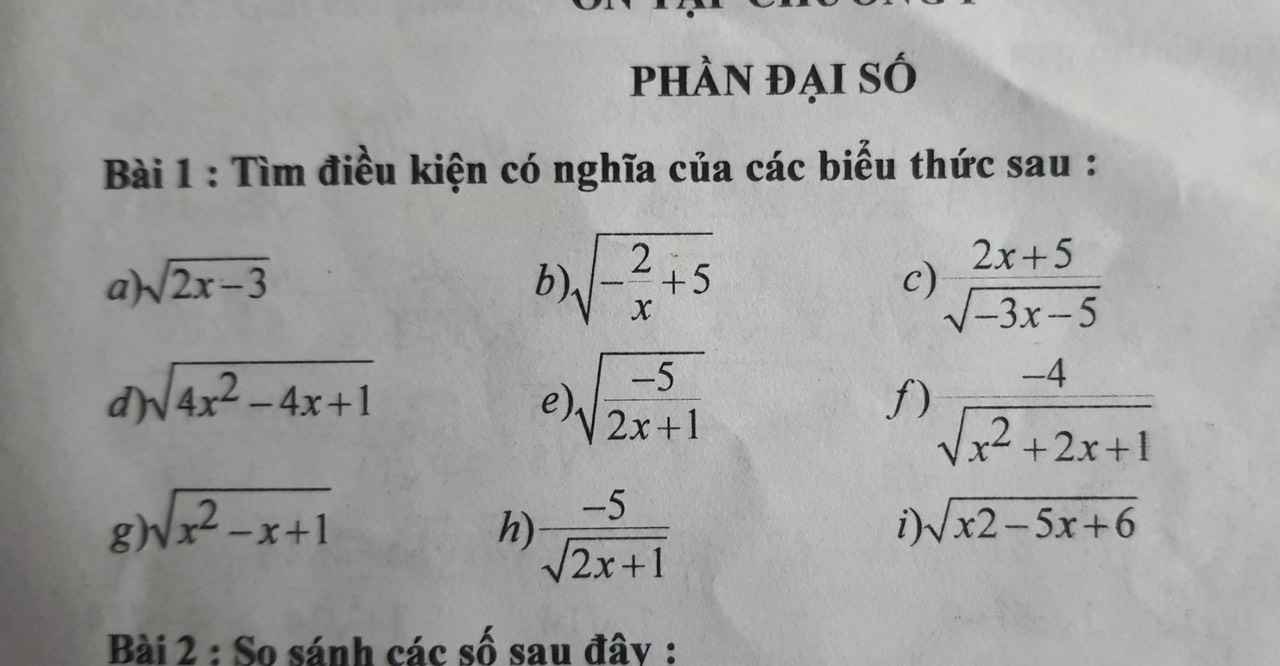
, mình đang cần giải gấp. Cảm ơn mn nhiều.
