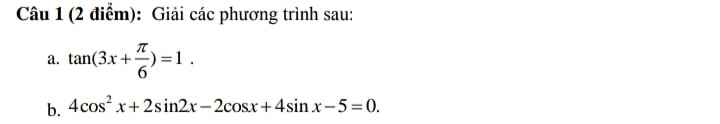1a.
$\tan (3x+\frac{\pi}{6})=1=\tan (\frac{\pi}{4})$
\(\Rightarrow 3x+\frac{\pi}{6}=\frac{\pi}{4}+k\pi\) với $k$ nguyên
\(\Leftrightarrow x=\frac{\pi}{36}+\frac{k}{3}\pi \) với $k$ nguyên.
1b.
$4\cos ^2x+2\sin 2x-2\cos x+4\sin x-5=0$
$\Leftrightarrow 4(1-\sin ^2x)+4\sin x\cos x-2\cos x+4\sin x-5=0$
$\Leftrightarrow -4\sin ^2x+4\sin x\cos x-2\cos x+4\sin x-1=0$
$\Leftrightarrow (4\sin x\cos x-2\cos x)-(4\sin ^2x-4\sin x+1)=0$
$\Leftrightarrow 2\cos x(2\sin x-1)-(2\sin x-1)^2=0$
$\Leftrightarrow (2\sin x-1)(2\cos x-2\sin x+1)=0$
Xét các TH sau:
TH1: $2\sin x=1\Rightarrow x=\frac{\pi}{6}+2k\pi$ hoặc $x=\frac{5\pi}{6}+2k\pi$ với $k$ nguyên
TH2: $2\cos x-2\sin x+1=0$
\(\Leftrightarrow 1-2\sin ^2\frac{x}{2}+2\cos ^2\frac{x}{2}-1-4\sin \frac{x}{2}\cos \frac{x}{2}+\sin ^2\frac{x}{2}+\cos ^2\frac{x}{2}=0\)
\(\Leftrightarrow 3\cos ^2\frac{x}{2}-\sin ^2\frac{x}{2}-4\sin \frac{x}{2}\cos \frac{x}{2}=0\)
Dễ thấy $\cos \frac{x}{2}\neq 0$ nên pt
\(\Leftrightarrow 3-\tan ^2\frac{x}{2}-4\tan \frac{x}{2}=0\)
\(\Rightarrow \tan \frac{x}{2}=-2\pm \sqrt{7}\)
\(\Rightarrow x=2\tan ^{-1}(-2\pm \sqrt{7})+2k\pi\) với $k$ nguyên