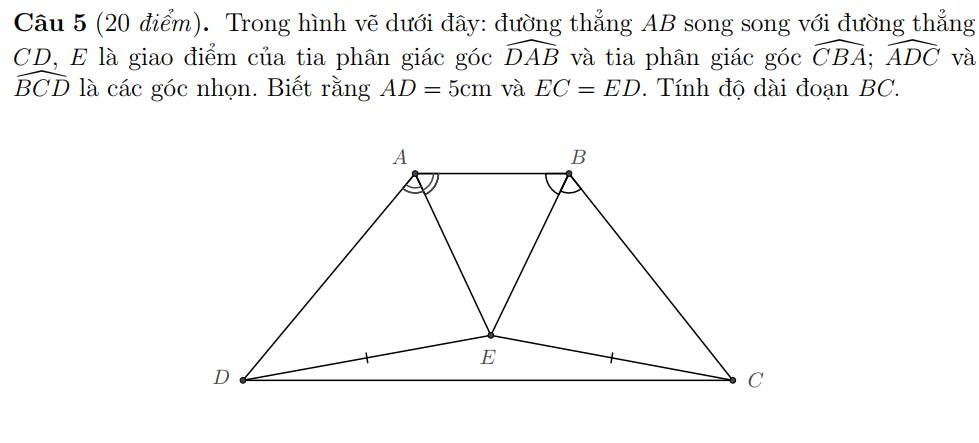
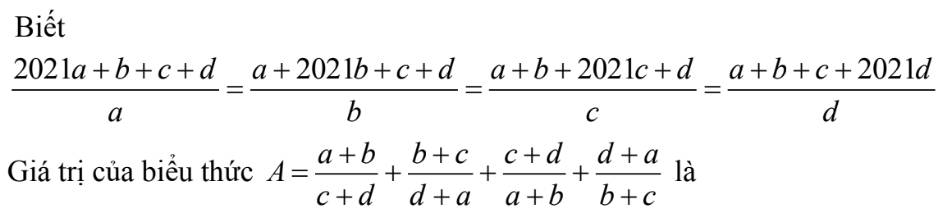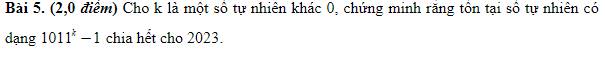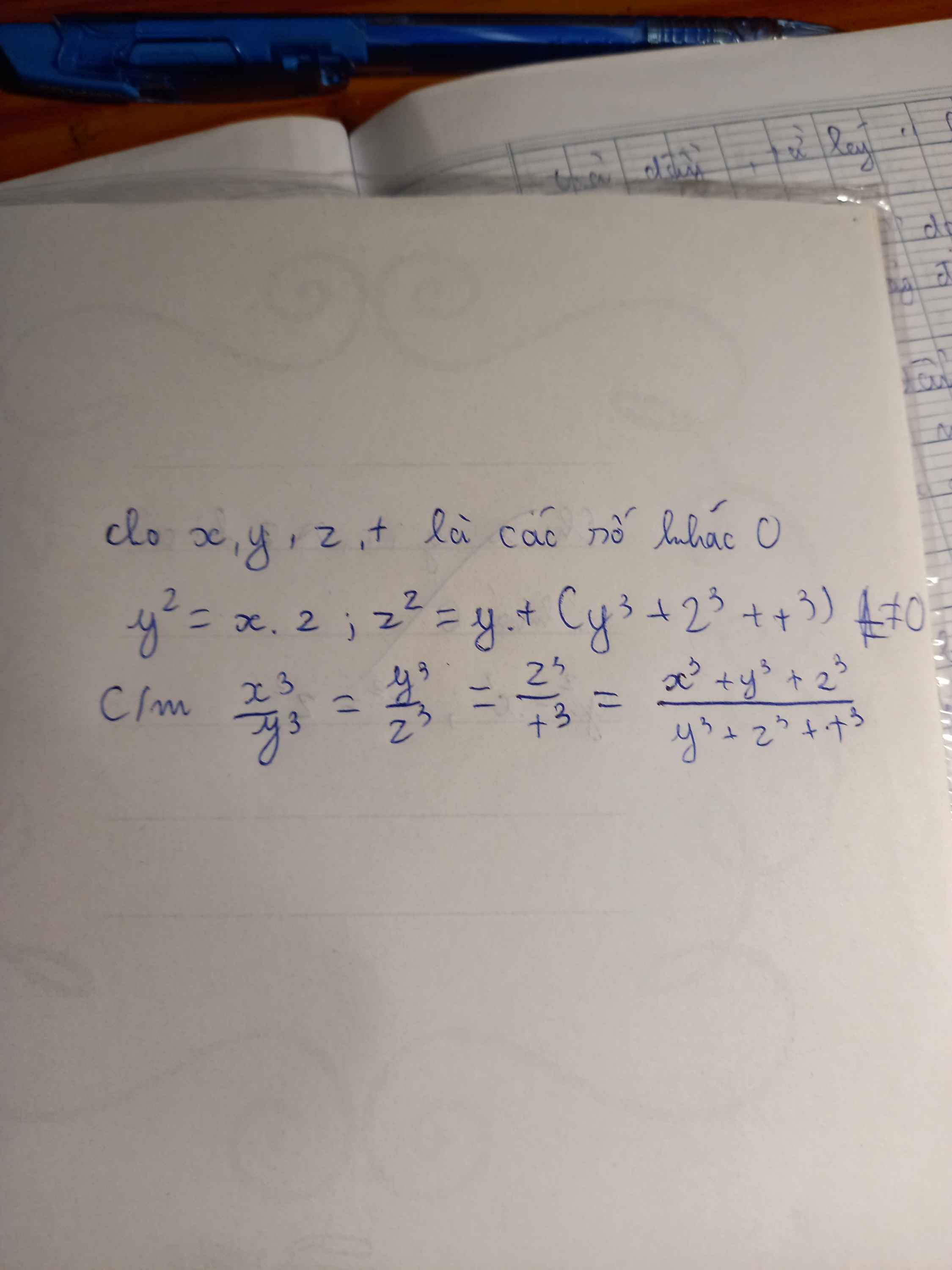Ta có: \(\frac{2021a+b+c+d}{a}=\frac{a+2021b+c+d}{b}=\frac{a+b+2021c+d}{c}=\frac{a+b+c+2021d}{d}\)
=>\(\frac{b+c+d}{a}+2021=\frac{a+c+d}{b}+2021=\frac{a+b+d}{c}+2021=\frac{a+b+c}{d}+2021\)
=>\(\frac{b+c+d}{a}=\frac{a+c+d}{b}=\frac{a+b+d}{c}=\frac{a+b+c}{d}\)
TH1: a+b+c+d<>0
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{b+c+d}{a}=\frac{a+c+d}{b}=\frac{a+b+d}{c}=\frac{a+b+c}{d}=\frac{b+c+d+a+c+d+a+b+d+a+b+c}{a+b+c+d}=\frac{3a+3b+3c+3d}{a+b+c+d}=3\)
=>\(\begin{cases}b+c+d=3a\\ a+c+d=3b\\ a+b+d=3c\\ a+b+c=3d\end{cases}\Rightarrow\begin{cases}b+c+d+a=4a\\ a+b+c+d=4b\\ a+b+c+d=4c\\ a+b+c+d=4d\end{cases}\)
=>a=b=c=d
Ta có: \(A=\frac{a+b}{c+d}+\frac{b+c}{d+a}+\frac{c+d}{a+b}+\frac{d+a}{b+c}\)
\(=\frac{a+a}{a+a}+\frac{b+b}{b+b}+\frac{c+c}{c+c}+\frac{d+d}{d+d}\)
=1+1+1+1
=4
TH2: a+b+c+d=0
=>a+b=-(c+d); b+c=-(a+d)
Ta có: \(A=\frac{a+b}{c+d}+\frac{b+c}{d+a}+\frac{c+d}{a+b}+\frac{d+a}{b+c}\)
\(=\frac{-\left(c+d\right)}{c+d}+\frac{-\left(a+d\right)}{a+d}+\frac{c+d}{-\left(c+d\right)}+\frac{d+a}{-\left(d+a\right)}\)
=-1-1-1-1
=-4