a: Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2=R^2\)
Ta có: ΔOAM vuông tại A
=>\(OA^2+AM^2=OM^2\)
=>\(AM^2=6^2-3^2=27\)
=>\(AM=\sqrt{27}=3\sqrt{3}\left(cm\right)\)
Xét ΔOAM vuông tại A có \(sinOMA=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{OMA}=30^0\)
Ta có: ΔOAM vuông tại A
=>\(\widehat{AOM}+\widehat{AMO}=90^0\)
=>\(\widehat{AOM}=60^0\)
b: Ta có: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)CD tại I
Xét tứ giác MAIO có \(\widehat{MAO}=\widehat{MIO}=90^0\)
nên MAIO là tứ giác nội tiếp
=>M,A,I,O cùng thuộc một đường tròn
c:
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
Xét ΔOIM vuông tại I và ΔOHK vuông tại H có
\(\widehat{IOM}\) chung
Do đó: ΔOIM đồng dạng với ΔOHK
=>\(\dfrac{OI}{OH}=\dfrac{OM}{OK}\)
=>\(OI\cdot OK=OH\cdot OM=OA^2=OC^2\)
=>\(\dfrac{OI}{OC}=\dfrac{OC}{OK}\)
Xét ΔOIC và ΔOCK có
\(\dfrac{OI}{OC}=\dfrac{OC}{OK}\)
\(\widehat{COI}\) chung
Do đó: ΔOIC đồng dạng với ΔOCK
=>\(\widehat{OIC}=\widehat{OCK}\)
=>\(\widehat{OCK}=90^0\)
=>KC là tiếp tuyến của (O)








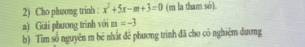
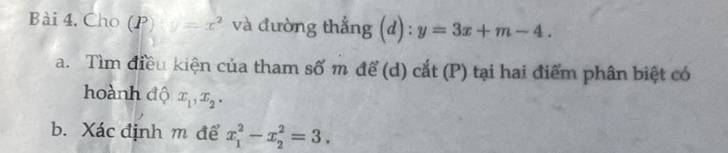


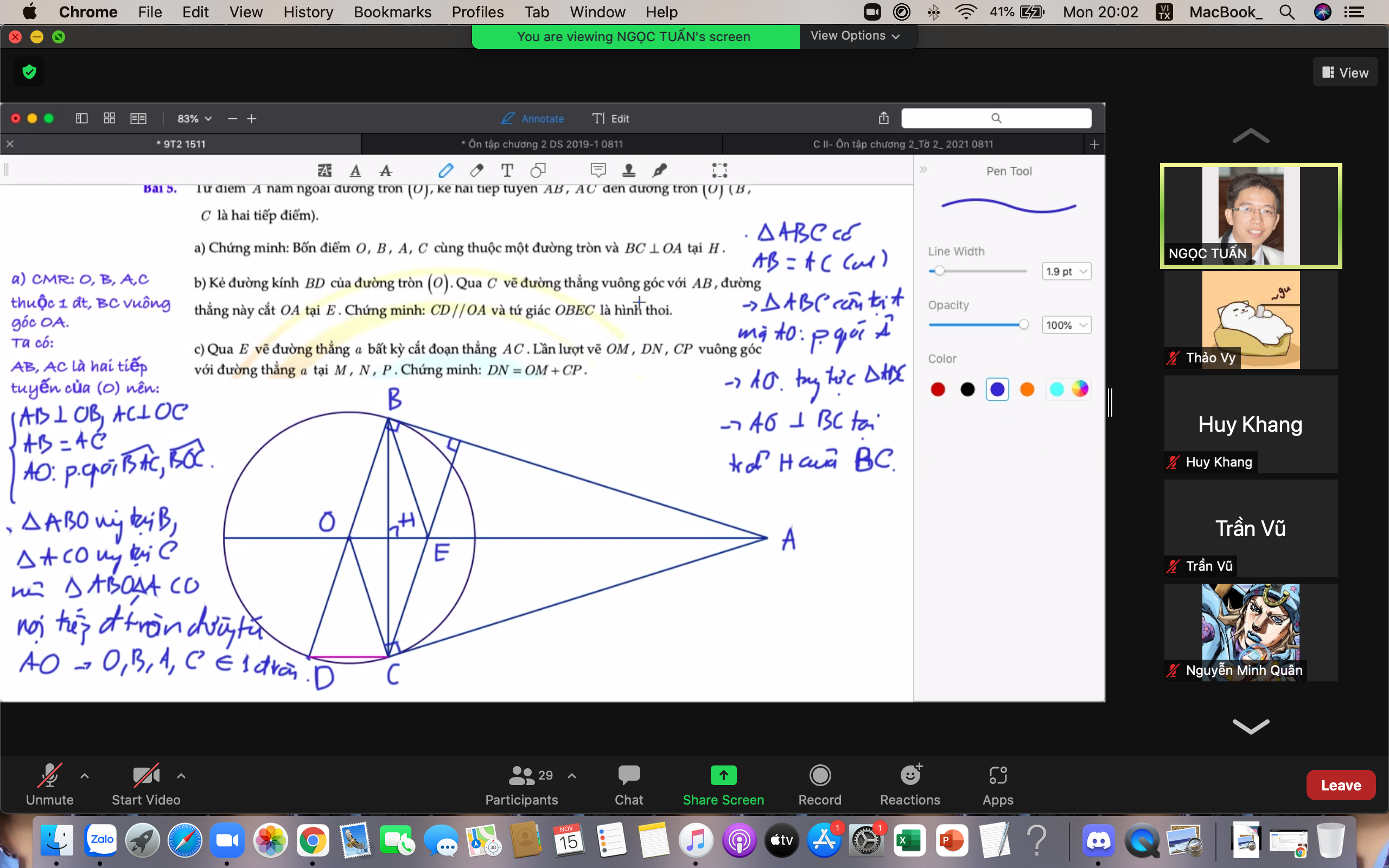

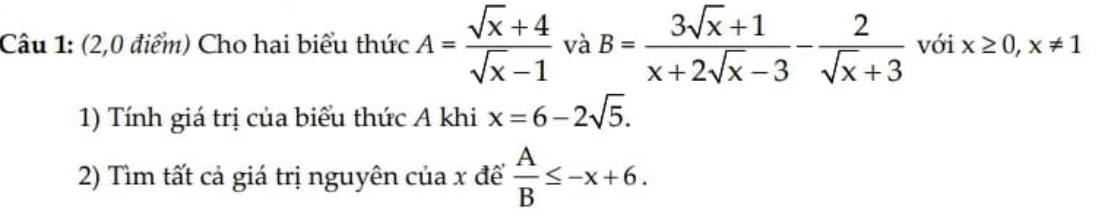
 giúp mình câu b với ạ
giúp mình câu b với ạ

