Phương trình đã cho có 2 nghiệm phân biệt khi:
\(\left\{{}\begin{matrix}m-2\ne0\\\Delta'=m^2-m\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m\ne2\end{matrix}\right.\)
b.
Theo hệ thức Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2m}{m-2}\\x_1x_2=\dfrac{m}{m-2}\end{matrix}\right.\)
\(Q=\dfrac{1}{x_1}+\dfrac{1}{x_2}+2017=\dfrac{x_1+x_2}{x_1x_2}+2017\)
\(=\dfrac{-2m}{m-2}.\dfrac{m-2}{m}+2017=-2+2017=2015\) là hằng số (đpcm)











 giúp mình 2 câu đầu với ạ
giúp mình 2 câu đầu với ạ giúp mình 2 câu này với ạ
giúp mình 2 câu này với ạ
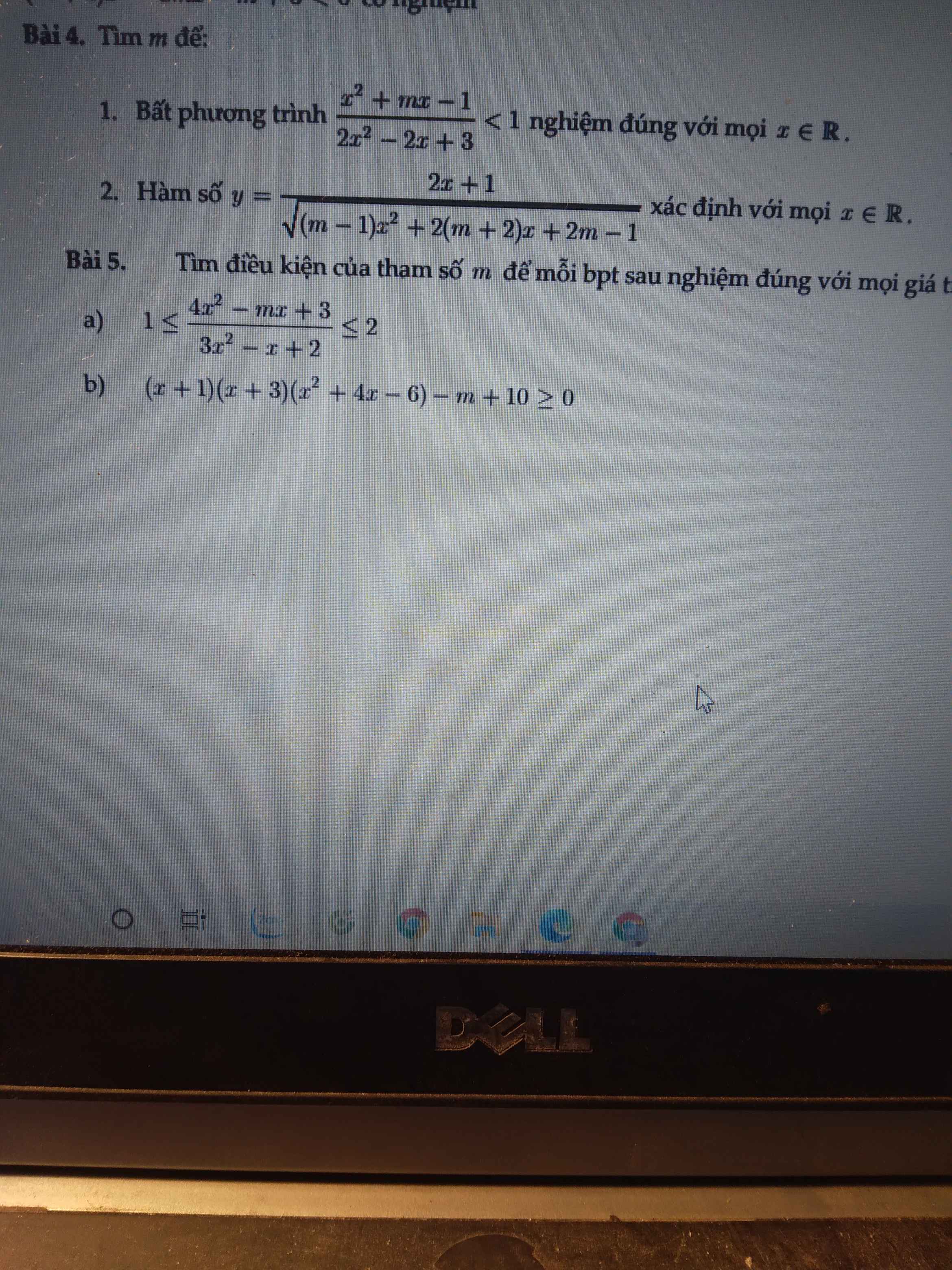



 giúp mình mấy câu này với mình cảm ơn nhìu ạ
giúp mình mấy câu này với mình cảm ơn nhìu ạ