Question

  Giúp mình câu 10 với các bạn

Answer 1

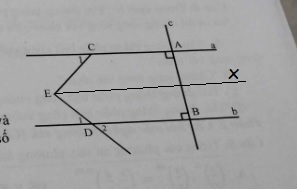
a.

Ta có \(\widehat{D_2}=\widehat{D_1}\) (hai góc đối đỉnh)

Mà \(\widehat{D_1}=50^0\)

Nên \(\widehat{D_2}=50^0\)

b.

Do \(\left\{{}\begin{matrix}a\perp c\\b\perp c\end{matrix}\right.\)

Suy ra \(a||b\)

c.

Do \(a||x\) nên \(\widehat{CEx}=\widehat{C_1}\) (hai góc so le trong)

Mà \(\widehat{C_1}=40^0\)

Suy ra \(\widehat{CEx}=40^0\)

Do \(\left\{{}\begin{matrix}a||x\\a||b\end{matrix}\right.\) nên \(b||x\)

Suy ra \(\widehat{DEx}=\widehat{D_1}\) (hai góc so le trong)

Suy ra \(\widehat{DEx}=50^0\)

Vậy \(\widehat{CED}=\widehat{CEx}+\widehat{DEx}=40^0+50^0=90^0\)