ĐKXĐ :\(\left\{{}\begin{matrix}x+1\ge0\\x^2+1\ge0\end{matrix}\right.\Leftrightarrow x\ge-1\)
Khi đó \((x^2+4x+5)\sqrt{x+1}=(3x^2-8x-5)\sqrt{x^2+1}\)
\(\Leftrightarrow(x^2+1)\sqrt{x+1}+4(x+1)\sqrt{x+1}=3(x^2+1)\sqrt{x^2+1}-8(x+1)\sqrt{x^2+1}\)
Đặt \(\sqrt{x+1}=a;\sqrt{x^2+1}=b(a\ge0;b>0)\)
Phương trình trở thành :
\(4a^3+ab^2=3b^3-8a^2b\)
\(\Leftrightarrow4(a^3+b^3)+b(8a^2+ab-7b^2)=0\)
\(\Leftrightarrow(a+b)(4a^2-4ab+4b^2)+(a+b)(8ab-7b^2)=0\)
\(\Leftrightarrow(a+b)(4a^2+4ab-3b^2)=0\)
\(\Leftrightarrow\left(a+b\right)\left(2a-b\right)\left(2a+3b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=0(\text{loại})\\2a-b=0\\2a+3b=0(\text{loại})\end{matrix}\right.\Leftrightarrow2a=b\) (vì \(\left\{{}\begin{matrix}a\ge0\\b>0\end{matrix}\right.\) nên a+b>0 ; 2a +3b > 0)
Trở lại cách đặt ta được
\(2\sqrt{x+1}=\sqrt{x^2+1}\Leftrightarrow x^2-4x-3=0\)
\(\Leftrightarrow x=\pm\sqrt{7}+2\) (loại \(x=-\sqrt{7}+2\))
Vậy x = \(\sqrt{7}+2\) là nghiệm phương trình

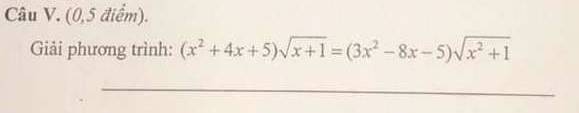






 được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều. 


 này được
này được 