\(a,P=x\left(3x+2\right)-x\left(x^2+3x\right)+x^3-2x+3\\ =3x^2+2x-x^3-3x^2+x^3-2x+3\\ =\left(3x^2-3x^2\right)+\left(x^3-x^3\right)+\left(2x-2x\right)+3=3\)
Vậy GT của biểu thức P không phụ thuộc vào biến x
\(b,Q=x\left(2x-3\right)+6x\left(\dfrac{1}{2}-\dfrac{1}{3}x\right)+1\\ =2x^2-3x+\dfrac{6x}{2}-\dfrac{6x^2}{3}+1\\ =2x^2-3x+3x-2x^2+1\\ =\left(2x^2-2x^2\right)+\left(3x-3x\right)+1=1\)
Vậy GT của biểu thức Q không phụ thuộc vào biến x
Đúng 3
Bình luận (0)
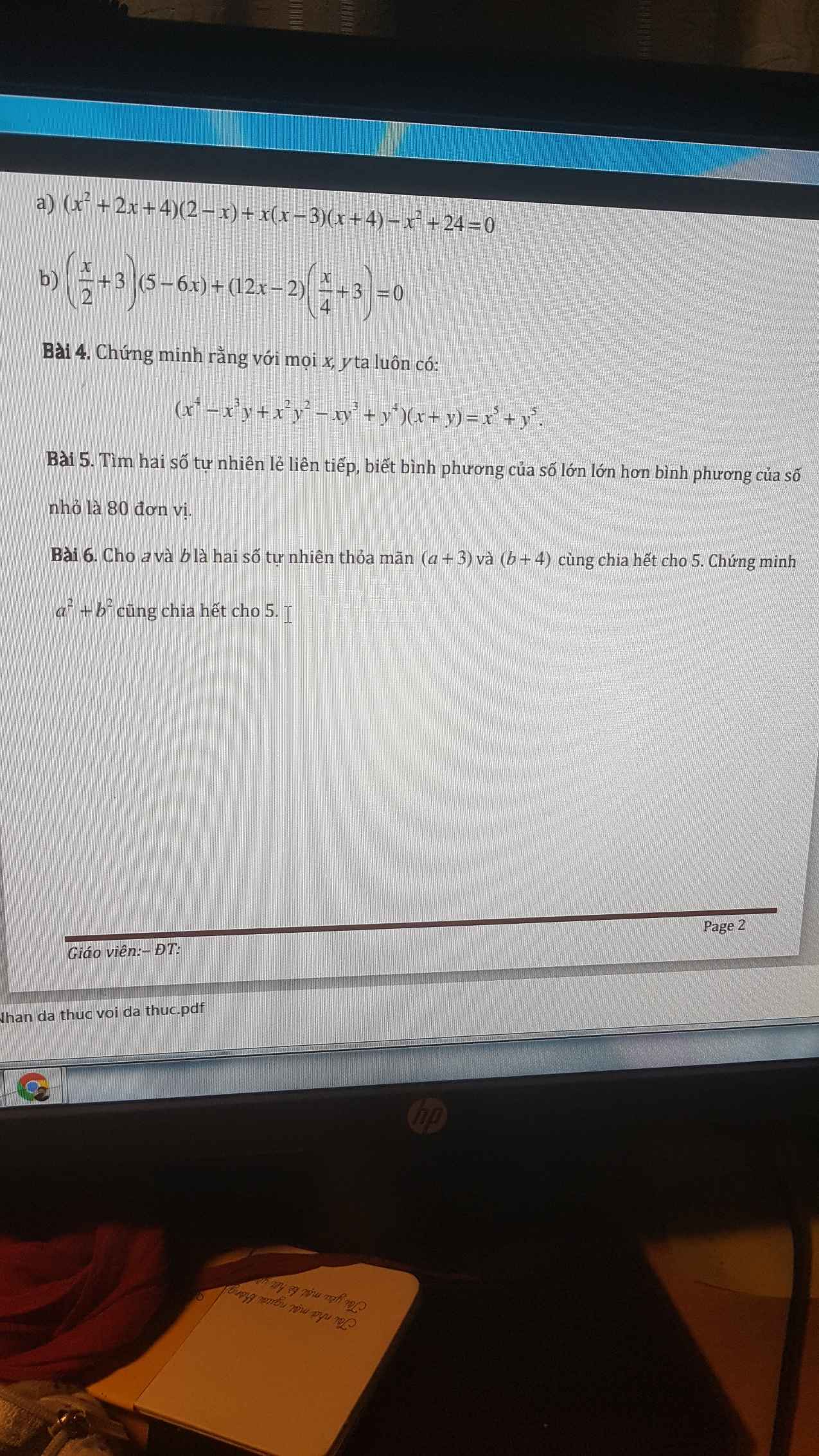
Mình cần giải bài 6 ạ, giúp mình với huhu ;-;
