Câu 1:
1.
a. $2x-4=0$
$\Leftrightarrow x=2$
b. $x^2-5x+4=0$
$\Leftrightarrow (x-1)(x-4)=0$
$\Rightarrow x-1=0$ hoặc $x-4=0$
$\Leftrightarrow x=1$ hoặc $x=4$
2.
\(\left\{\begin{matrix} 2x+y=1\\ x-3y=4\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2x+y=1\\ 2x-6y=8\end{matrix}\right.\)
\(\Rightarrow 7y=-7\) (trừ theo vế 2 PT)
$\Leftrightarrow y=-1$
$x=4+3y=4+3(-1)=1$
Câu 2.
1.
\(P=\left[\frac{(\sqrt{a}+1)(\sqrt{a}+2)}{(\sqrt{a}+2)(\sqrt{a}-1)}-\frac{\sqrt{a}(\sqrt{a}+1)}{(\sqrt{a}+1)(\sqrt{a}-1)}\right]:\frac{2\sqrt{a}}{(\sqrt{a}-1)(\sqrt{a}+1)}\)
\(=\left(\frac{\sqrt{a}+1}{\sqrt{a}-1}-\frac{\sqrt{a}}{\sqrt{a}-1}\right).\frac{(\sqrt{a}-1)(\sqrt{a}+1)}{2\sqrt{a}}=\frac{1}{\sqrt{a}-1}.\frac{(\sqrt{a}-1)(\sqrt{a}+1)}{2\sqrt{a}}=\frac{\sqrt{a}+1}{2\sqrt{a}}\)
2.
Để \(P=\frac{\sqrt{a}+1}{2\sqrt{a}}=\frac{2\sqrt{a}-1}{4}\)
\(\Leftrightarrow 4(\sqrt{a}+1)=2\sqrt{a}(2\sqrt{a}-1)=4a-2\sqrt{a}\)
\(\Leftrightarrow 4a-6\sqrt{a}-4=0\)
\(\Leftrightarrow 2a-3\sqrt{a}-2=0\Leftrightarrow (\sqrt{a}-2)(2\sqrt{a}+1)=0\)
\(\Rightarrow \sqrt{a}=2\Leftrightarrow a=4\) (thỏa ĐKXĐ)
Câu 3.
1.
PT hoành độ giao điểm:
$(m-3)x+16-(x+m^2)=0$
$\Leftrightarrow (m-4)x=m^2-16(*)$
Để $(d),(d')$ cắt nhau tại 1 điểm trên trục tung thì PT $(*)$ nhận $x=0$ là nghiệm.
Điều này xảy ra khi $m=\pm 4$
Với $m=4$ thì $(d)\equiv (d')$ (loại). Do đó $m=-4$
2.
\(\Delta'=(m-2)^2+m^2=2m^2-4m+4=2(m-1)^2+2>0\)với mọi $m\in\mathbb{R}$ nên pt luôn có 2 nghiệm pb với mọi $m\in\mathbb{R}$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2(2-m)\\ x_1x_2=-m^2\end{matrix}\right.\)
Vì $x_1x_2=-m^2\leq 0$ mà $x_1<x_2$ nên:
$|x_1|=-x_1; |x_2|=x_2$. Do đó:
$|x_1|-|x_2|=6$
$\Leftrightarrow -x_1-x_2=6$
$\Leftrightarrow 2(2-m)=-6$
$\Leftrightarrow m=5$
Câu 5.
\(T=a-\frac{9ab^2}{1+9b^2}+b-\frac{9bc^2}{1+9c^2}+c-\frac{9ca^2}{1+9a^2}\)
\(=(a+b+c)-9\left(\frac{ab^2}{1+9b^2}+\frac{bc^2}{1+9c^2}+\frac{ca^2}{1+9a^2}\right)\)
\(\geq 1-9\left(\frac{ab^2}{6b}+\frac{bc^2}{6c}+\frac{ca^2}{6a}\right)\) (BĐT AM-GM)
\(=1-\frac{3}{2}(ab+bc+ac)\)
\(\geq 1-\frac{1}{2}(a+b+c)^2=1-\frac{1}{2}=\frac{1}{2}\)
Vậy $T_{\min}=\frac{1}{2}$. Giá trị này đạt tại $a=b=c=\frac{1}{3}$










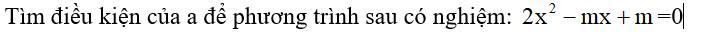



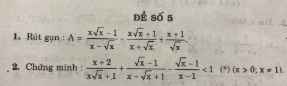 Mn giúp mình bài 2 vs ạ
Mn giúp mình bài 2 vs ạ