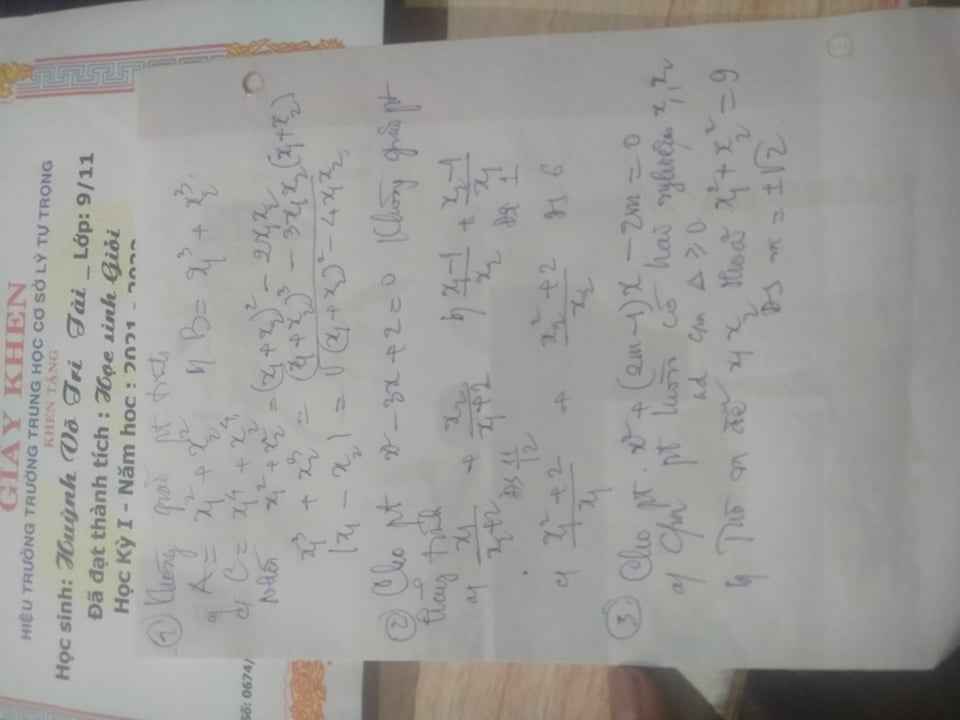3.1
\(\frac{3+\sqrt{3}}{1+\sqrt{3}}=\frac{\sqrt{3}(\sqrt{3}+1)}{\sqrt{3}+1}=\sqrt{3}\)
3.2
\(=\frac{4(\sqrt{5}-1)-4(\sqrt{5}+1)}{(\sqrt{5}-1)(\sqrt{5}+1)}:\sqrt{(\sqrt{2}+1)^2}\)
\(=\frac{-8}{4}:(\sqrt{2}+1)=\frac{-2}{\sqrt{2}+1}=\frac{-2(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}=\frac{-2(\sqrt{2}-1)}{1}=2(1-\sqrt{2})\)
3.3.
\(=\frac{\sqrt{2}+1-(\sqrt{2}-1)}{(\sqrt{2}-1)(\sqrt{2}+1)}:\sqrt{(\sqrt{2}-1)^2}=\frac{2}{1}:(\sqrt{2}-1)=\frac{2}{\sqrt{2}-1}=\frac{2(\sqrt{2}+1)}{(\sqrt{2}-1)(\sqrt{2}+1)}=2(\sqrt{2}+1)\)
3.4 Cái này đã gọn lắm rồi không cần rút gọn nữa.
3.5
\(=\frac{(\sqrt{5}+\sqrt{3})^2+(\sqrt{5}-\sqrt{3})^2}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}=\frac{16}{5-3}=8\)
3.6
\(=\frac{(\sqrt{5}-1)^2-(\sqrt{5}+1)^2}{(\sqrt{5}+1)(\sqrt{5}-1)}=\frac{-4\sqrt{5}}{5-1}=-\sqrt{5}\)





 Giúp mình bài 2b với bài 3 với ạ
Giúp mình bài 2b với bài 3 với ạ




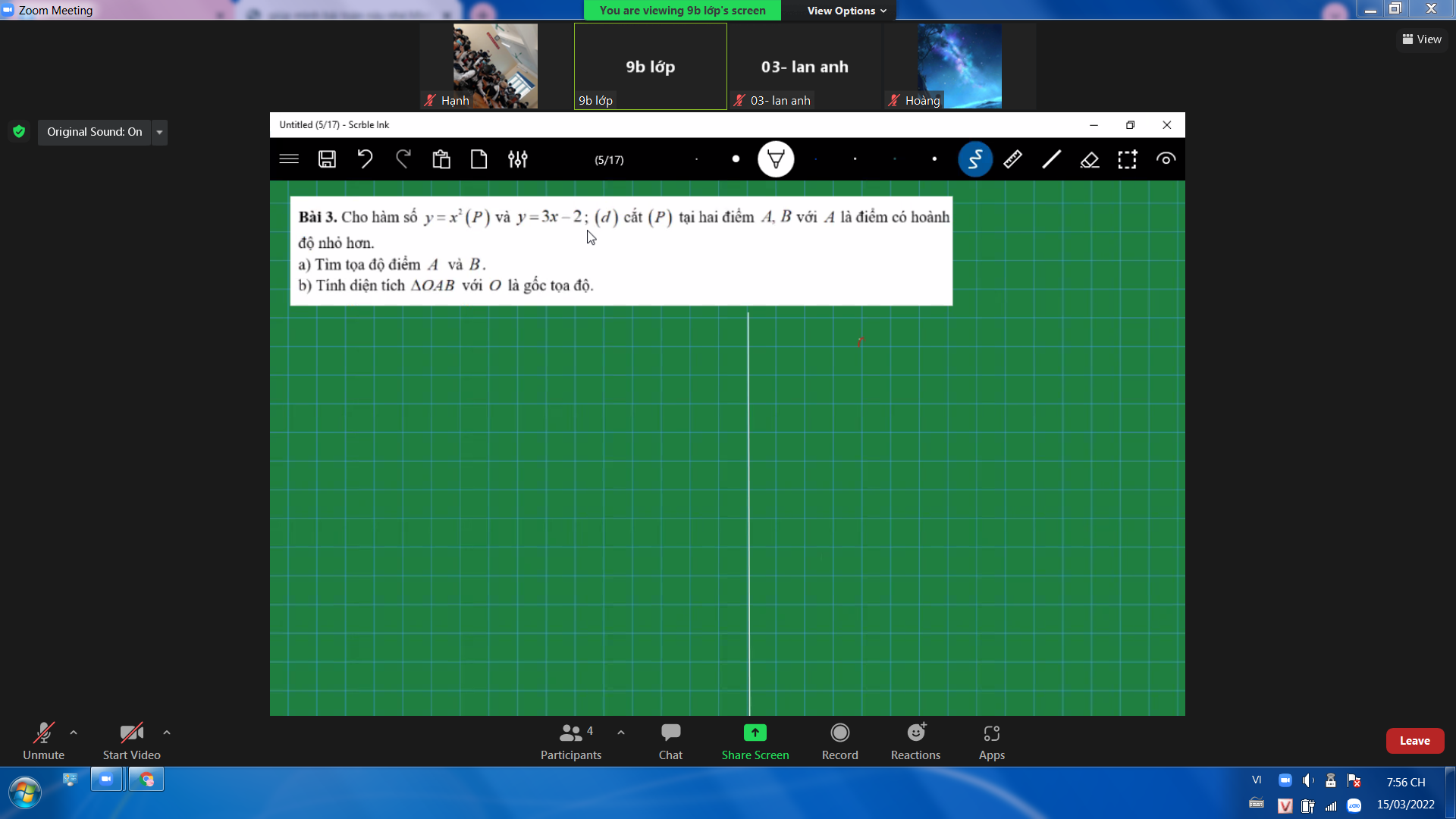

 giúp mình bài 3 với ạ
giúp mình bài 3 với ạ