Bài 2:
ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
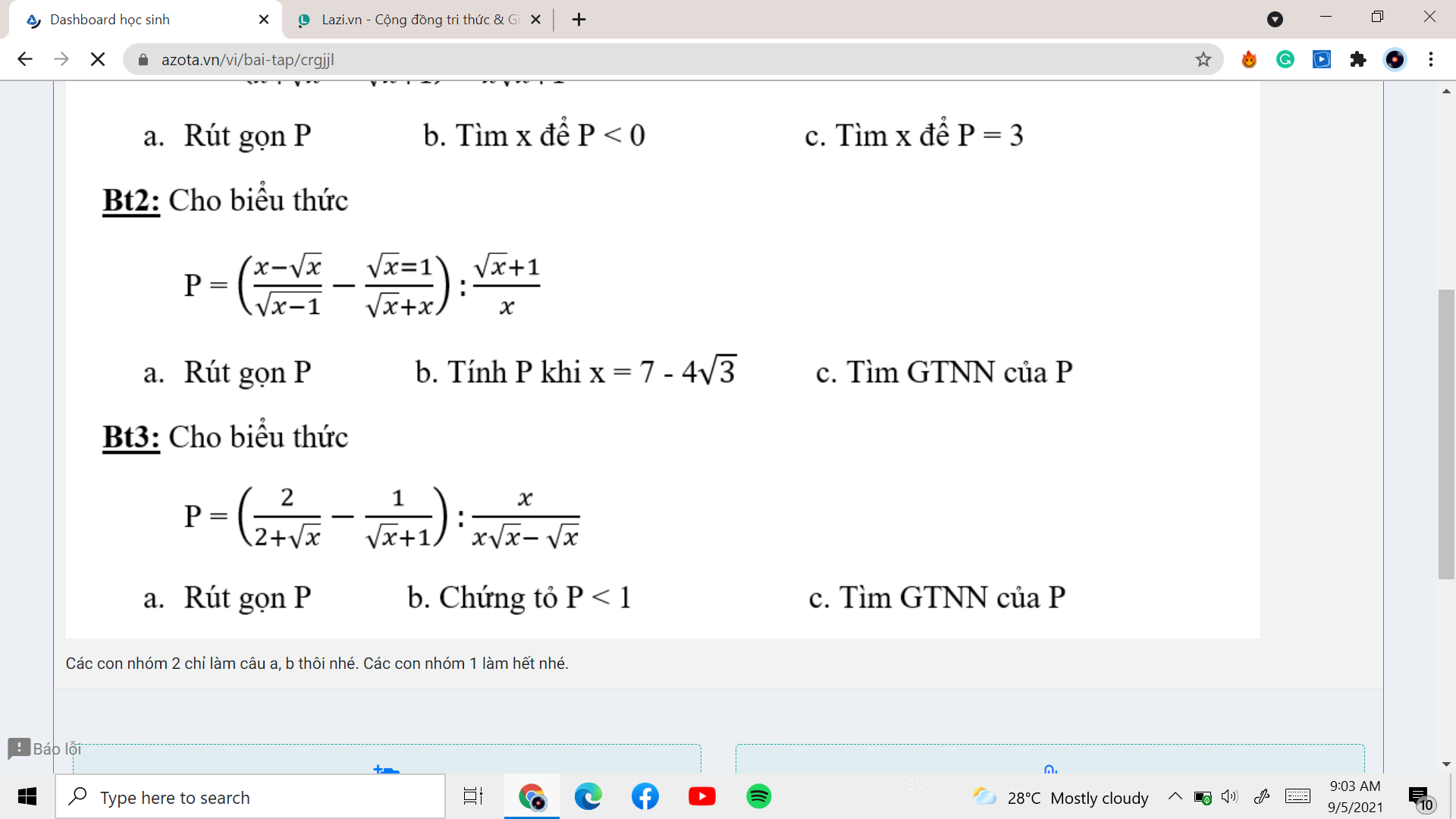
\(P=\left(\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+x}\right):\dfrac{\sqrt{x}+1}{x}\)
\(P=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}+1}{x}\)
\(P=\left(\sqrt{x}-\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}+1}{x}\)
\(P=\left(\dfrac{\sqrt{x}.\sqrt{x}.\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}+1}{x}\)
\(P=\dfrac{x.\left(\sqrt{x}+1\right)-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}+1}{x}\)
\(P=\dfrac{\left(x-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{x}{\sqrt{x}+1}\)
\(P=\dfrac{x-1}{\sqrt{x}}.\dfrac{x}{\sqrt{x}+1}\)
\(P=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}.\dfrac{\sqrt{x^2}}{\sqrt{x}+1}\)
\(P=\left(\sqrt{x}-1\right).\sqrt{x}\)
\(P=x-\sqrt{x}\)














 Mn giúp mình bài 2 vs ạ
Mn giúp mình bài 2 vs ạ
 giúp mình bài 3 câu 2 ạ
giúp mình bài 3 câu 2 ạ






