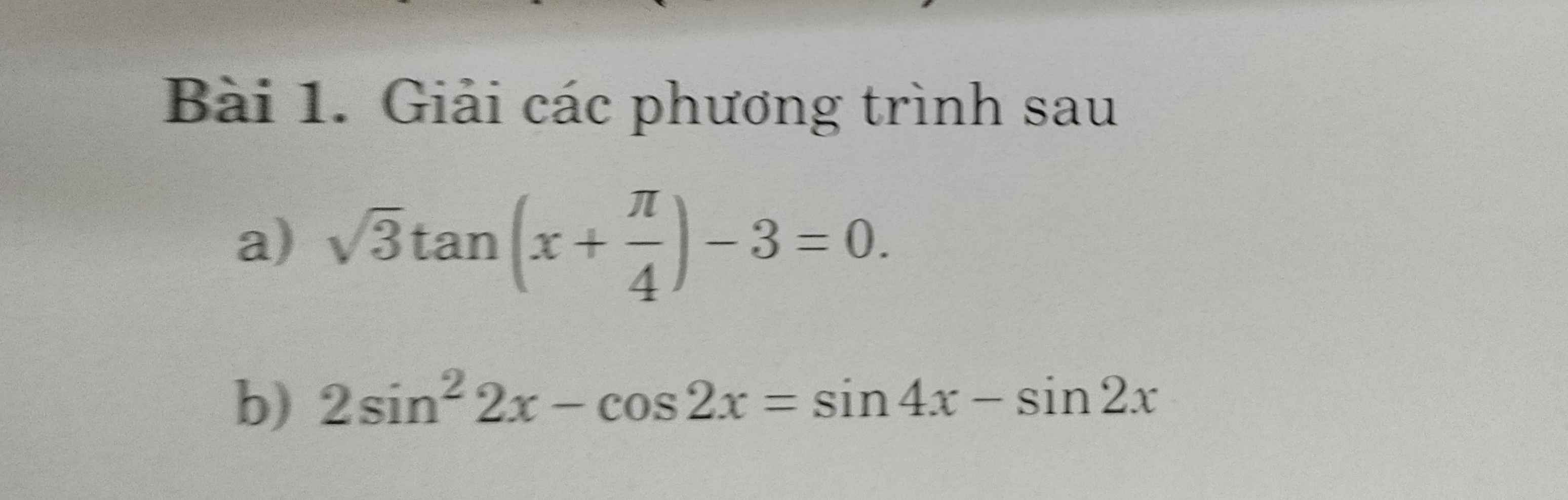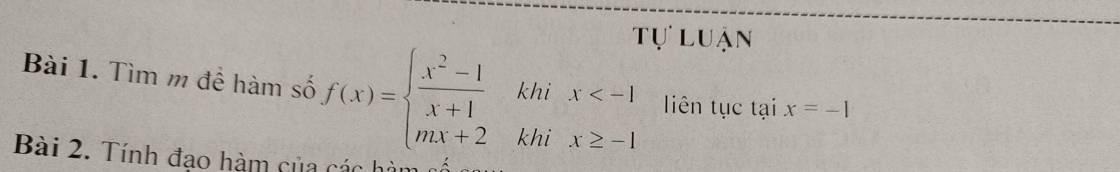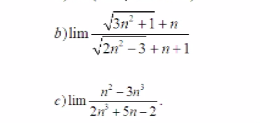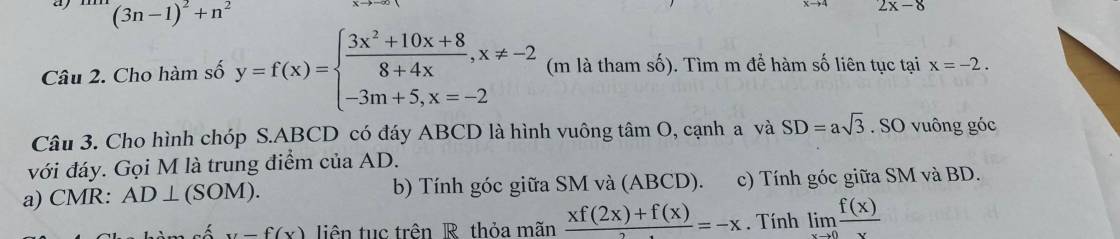Lời giải:
$2\sin ^22x-\cos 2x=\sin 4x-\sin 2x$
$\Leftrightarrow 2\sin^22x-\cos 2x=2\sin 2x\cos 2x-\sin 2x$
$\Leftrightarrow (2\sin ^22x+\sin 2x)-(\cos 2x+2\sin 2x\cos 2x)=0$
$\Leftrightarrow \sin 2x(2\sin 2x+1)-\cos 2x(1+2\sin 2x)=0$
$\Leftrightarrow (2\sin 2x+1)(\sin 2x-cos 2x)=0$
$\Rightarrow \sin 2x=\frac{-1}{2}$ hoặc $\sin 2x=\cos 2x$
$\Rightarrow \sin 2x=\frac{-1}{2}$ hoặc $\sin 2x=\sin (\frac{\pi}{2}-2x)$
Đến đây thì đơn giản rồi.
Đúng 0
Bình luận (0)