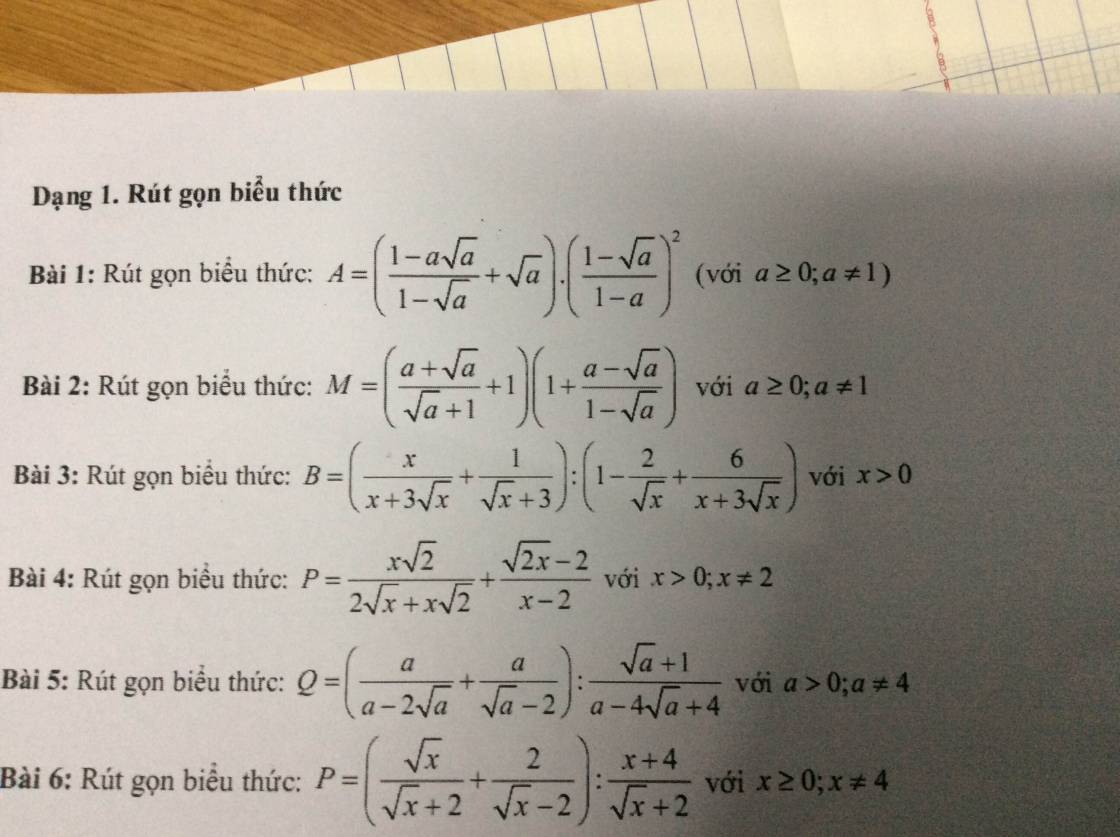\(Bài2\\ M=\left(\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}+1}+1\right)\left(1+\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{1-\sqrt{a}}\right)\\ =\left(\sqrt{a}+1\right)\left(1+\dfrac{-\sqrt{a}\left(1-\sqrt{a}\right)}{1-\sqrt{a}}\right)\\ =\left(\sqrt{a}+1\right)\left(1-\sqrt{a}\right)=1-a\)
\(-------------------\\ Bài3\\ B=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}+3\right)}+\dfrac{1}{\sqrt{x}+3}\right):\left(1-\dfrac{2}{\sqrt{x}}+\dfrac{6}{\sqrt{x}\left(\sqrt{x}+3\right)}\right)\\ =\left(\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}\right):\left(\dfrac{x+3\sqrt{x}-2\left(\sqrt{x}+3\right)+6}{\sqrt{x}\left(\sqrt{x}+3\right)}\right)\\ =\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}:\dfrac{x+3\sqrt{x}-2\sqrt{x}-6+6}{\sqrt{x}\left(\sqrt{x}+3\right)}\\ =\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{x+\sqrt{x}}=1\)