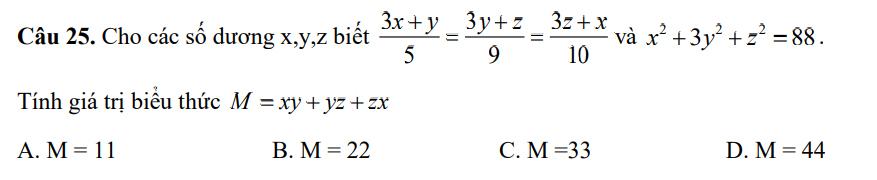Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k\\y=3k\end{matrix}\right.\)
Ta có: \(x^2+2xy=16\)
\(\Leftrightarrow4k^2+2\cdot2k\cdot3k=16\)
\(\Leftrightarrow k^2=1\)
Trường hợp 1: k=1
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k=2\\y=3k=3\end{matrix}\right.\)
Trường hợp 2: k=-1
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k=-2\\y=3k=-3\end{matrix}\right.\)

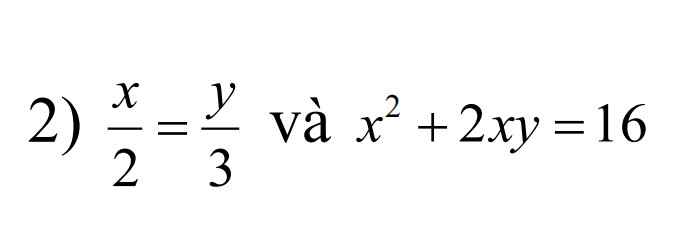












 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ