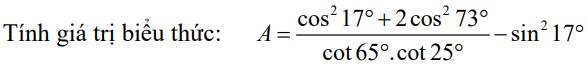a.
\(a+\dfrac{1}{\left(a-b\right)b}=\left(a-b\right)+\dfrac{1}{\left(a-b\right).b}+b\ge3\sqrt[3]{\dfrac{\left(a-b\right).1.b}{\left(a-b\right).b}}=3\) (đpcm)
b.
\(a+\dfrac{1}{\left(a-b\right)\left(b+1\right)}=\left(a-b\right)+\dfrac{1}{\left(a-b\right)\left(b+1\right)}+\left(b+1\right)-1\ge3\sqrt[3]{\dfrac{\left(a-b\right)\left(b+1\right)}{\left(a-b\right)\left(b+1\right)}}-1=2\)
c.
\(a+\dfrac{4}{\left(a-b\right)\left(b+1\right)^2}=a-b+\dfrac{4}{\left(a-b\right)\left(b+1\right)^2}+b\ge2\sqrt{\dfrac{4\left(a-b\right)}{\left(a-b\right)\left(b+1\right)^2}}+b\)
\(=\dfrac{4}{b+1}+b=\left(\dfrac{4}{b+1}+b+1\right)-1\ge2\sqrt{\dfrac{4\left(b+1\right)}{b+1}}-1=3\)

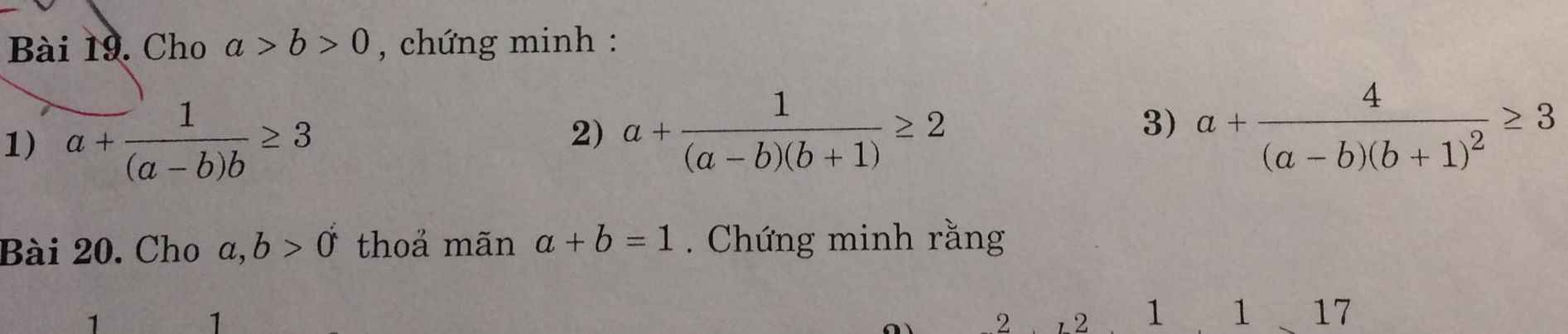 giúp mik vs mng
giúp mik vs mng





 giúp mik vs mng ơi.mik cần gấp á
giúp mik vs mng ơi.mik cần gấp á