\(1,=\dfrac{\sqrt{7}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=\sqrt{7}\\ 6,=\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{-3\left(\sqrt{3}-1\right)}=\dfrac{-\sqrt{2}}{3}\\ 2,=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}}=\sqrt{3}-1\\ 7,=\dfrac{3\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}=3\\ 3,=\dfrac{\sqrt{2}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}=\sqrt{2}\\ 8,=\dfrac{\sqrt{10}\left(\sqrt{2}+\sqrt{5}\right)}{2\sqrt{10}}=\dfrac{\sqrt{2}+\sqrt{5}}{2}\\ 4,=\dfrac{\sqrt{2}\left(\sqrt{5}-1\right)}{-\left(\sqrt{5}-1\right)}=-\sqrt{2}\\ 9,=\dfrac{\sqrt{6}\left(\sqrt{3}-\sqrt{2}\right)}{\sqrt{3}-\sqrt{2}}=\sqrt{6}\\ 5,=\dfrac{\sqrt{7}\left(\sqrt{7}-1\right)}{3\sqrt{7}}=\dfrac{\sqrt{7}-1}{3}\\ 10,=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)=9-2=7\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
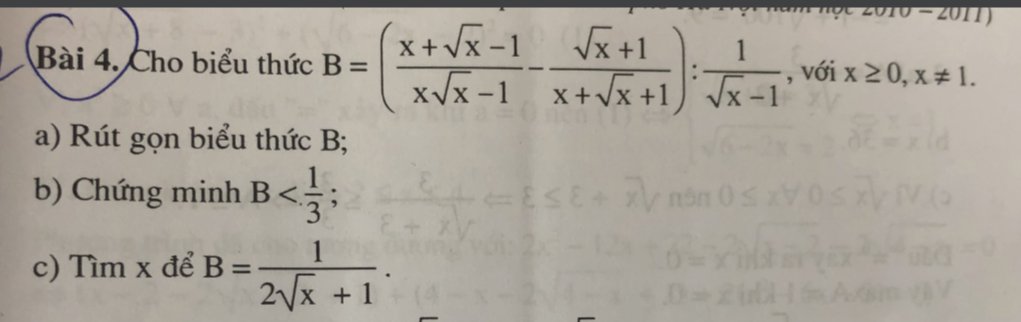
Giúp mik vs ạ mik cảm ơn!
giúp mik vs ạ mik cần gấp , mik cảm ơn

Giúp mik bài 2 vs. Mik cảm ơn

giúp mik vs ạ mik đang cần gấp . mik cảm ơn
Nhờ mn giúp mik vs ạ. Mik cảm ơn.
Giúp mik vs ah
Mik đang cần gấp
Cảm ơn ạ
Giúp mik bài 4,5 vs ạ
Mik cảm ơn nhiều😊
giải giúp mik bài c3c.48 và 49 vs ạ
mik cảm ơn
chứng minh y=3x
\(\dfrac{y+6x}{y}\)= \(\dfrac{y}{x}\)
giải giúp mik vs ạ mik cảm ơn ạ











