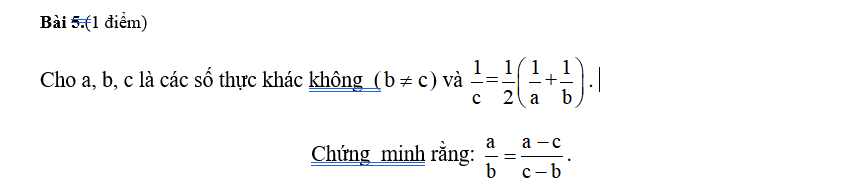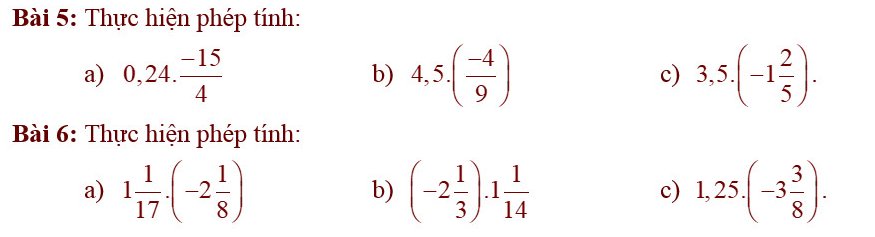Đặt \(A=\dfrac{1}{1.2}+\dfrac{1}{3.4}+...+\dfrac{1}{99.10}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{99}-\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)\)
Thêm bớt vào tổng trên đại lượng \(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100}\) ta được:
\(A=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{99}+\dfrac{1}{100}-2.\left(\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{100}\right)\)
\(=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{50}+\dfrac{1}{51}+...+\dfrac{1}{100}-\left(1+\dfrac{1}{2}+...+\dfrac{1}{50}\right)\)
\(=\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{100}\)
\(\Rightarrow B=\dfrac{\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{100}}{\dfrac{1}{51}+\dfrac{1}{52}+...+\dfrac{1}{100}}=1\)

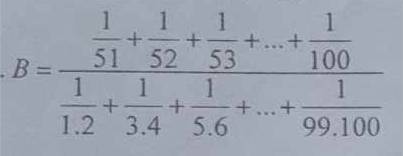



 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ