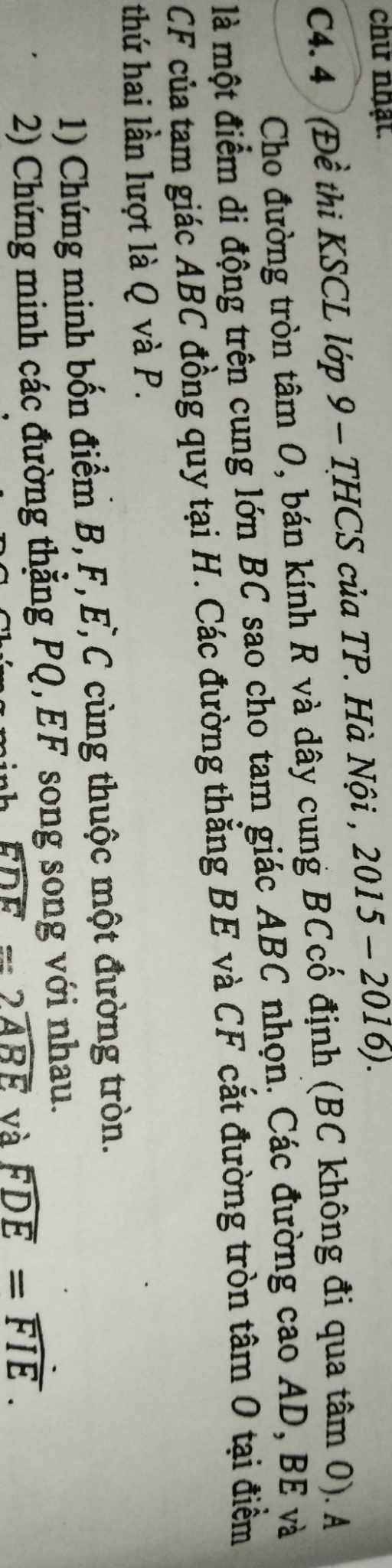1: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>B,F,E,C cùng thuộc một đường tròn
2: ta có: BFEC là tứ giác nội tiếp
=>\(\widehat{EFC}=\widehat{EBC}\)
=>\(\widehat{HFE}=\widehat{QBC}\left(1\right)\)
Xét (O) có
\(\widehat{QBC}\) là góc nội tiếp chắn cung QC
\(\widehat{QPC}\) là góc nội tiếp chắn cung QC
Do đó: \(\widehat{QBC}=\widehat{QPC}\)
=>\(\widehat{QBC}=\widehat{HPQ}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{HFE}=\widehat{HPQ}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên FE//PQ