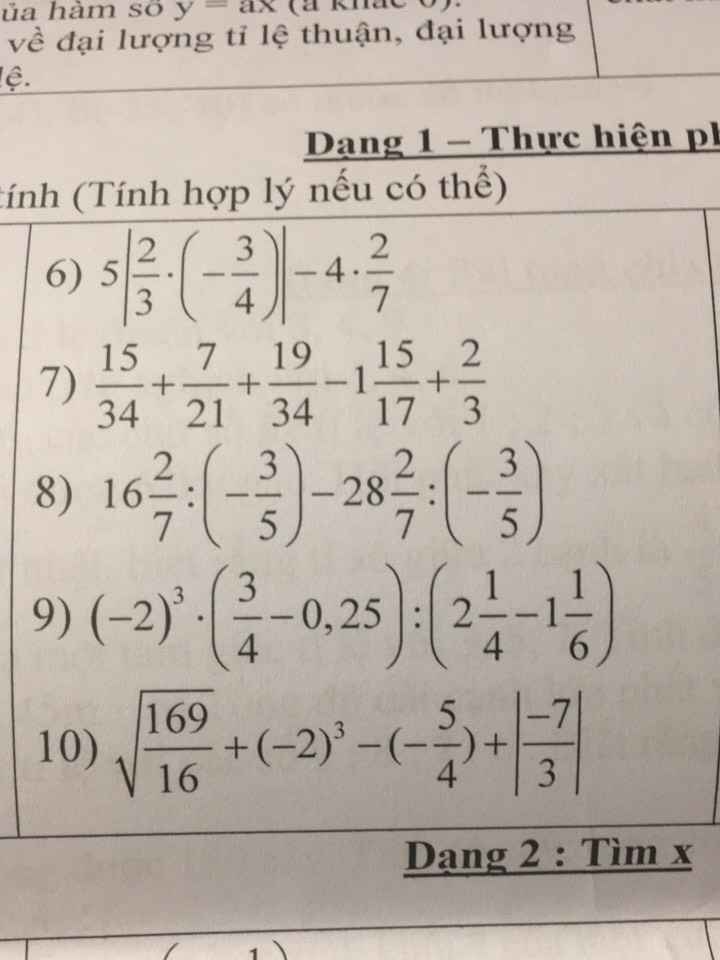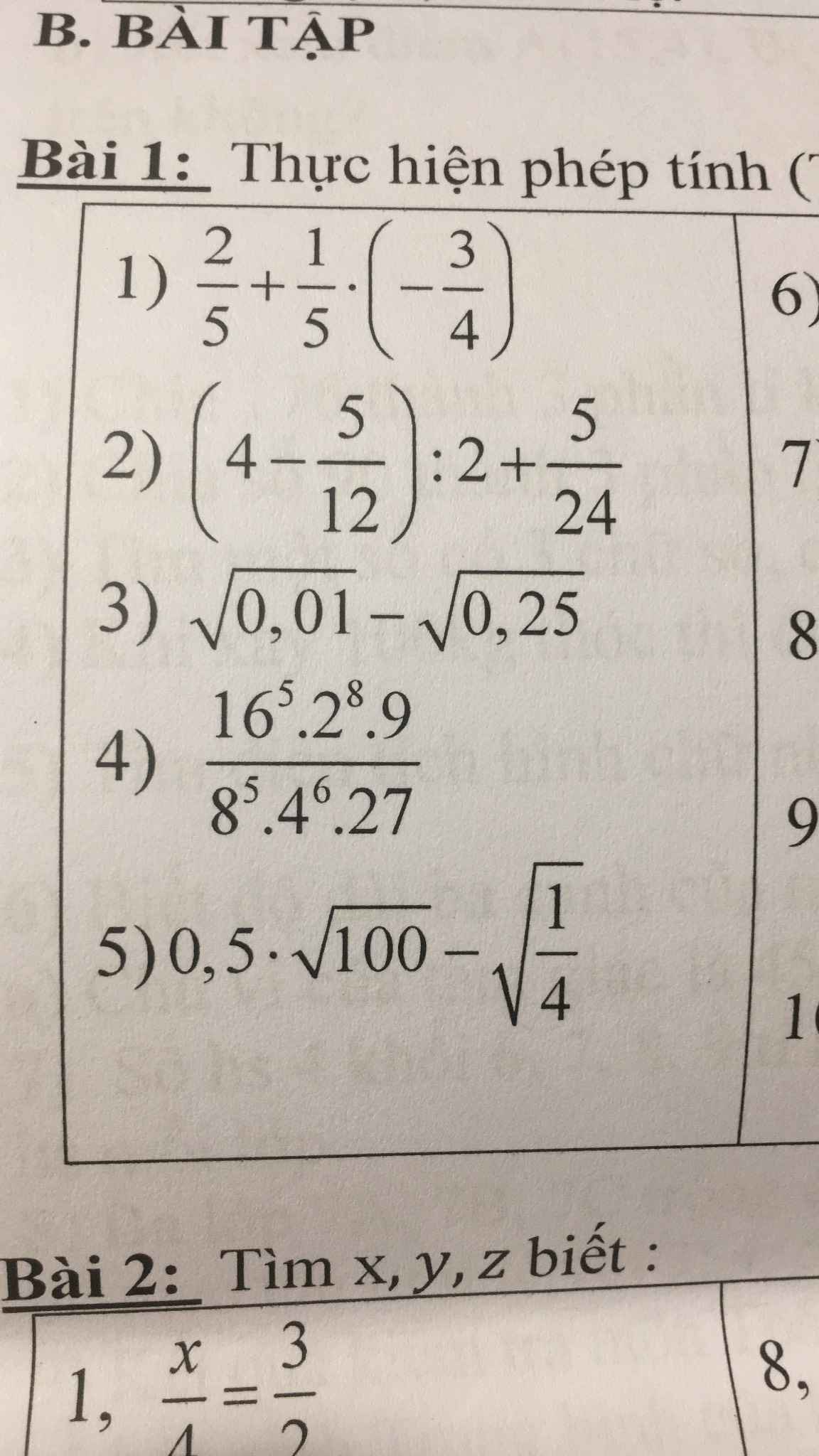a) Thu gọn và sắp xếp:
\(A\left(x\right)=9x^5-x^3+4x^2+9x-x^2+9-9x^5+x^3-3\)
\(=\left(9x^5-9x^5\right)+\left(-x^3+x^3\right)+\left(4x^2-x^2\right)+9x+\left(9-3\right)\)
\(=0+0+3x^2+9x+6\)
\(=3x^2+9x+6\)
b) Bậc của A(x) là 2
Hệ số tự do của A(x) là 6
Hệ số cao nhất của A(x) là 1
c) Ta có:
\(A\left(2\right)=3\cdot2^2+9\cdot2+6=36\)
\(A\left(-1\right)=3\cdot\left(-1\right)^2+9\cdot\left(-1\right)+6=0\)
\(A\left(0\right)=6\)
d) \(A\left(\dfrac{1}{2}\right)=3\cdot\left(\dfrac{1}{2}\right)^2+9\cdot\dfrac{1}{2}+6=\dfrac{45}{4}\)
\(A\left(-2\right)=3\cdot\left(-2\right)^2+9\cdot\left(-2\right)+6=0\)
\(A\left(-1\right)=0\) (ở câu c)
Vậy \(-2;-1\) là nghiệm của đa thức

 giúp mik vs ạ, mik cần gấp!
giúp mik vs ạ, mik cần gấp!



 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ


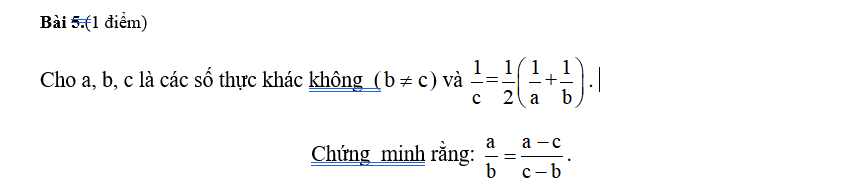


 mn giúp mik vs ạ. Mik đang cần gấp
mn giúp mik vs ạ. Mik đang cần gấp
 giúp mik vs ạ mik đag cần gấp pls
giúp mik vs ạ mik đag cần gấp pls