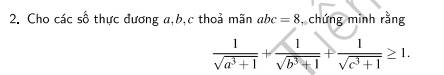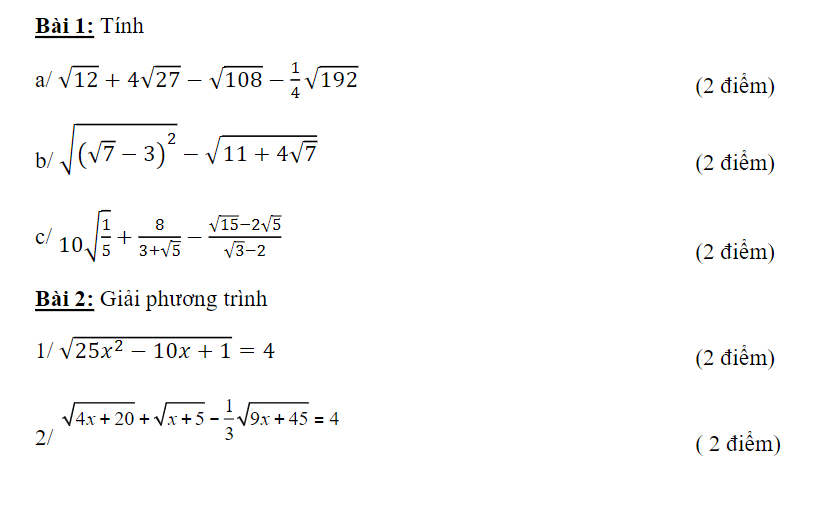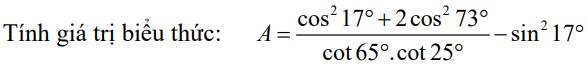a. Em tự giải
b.
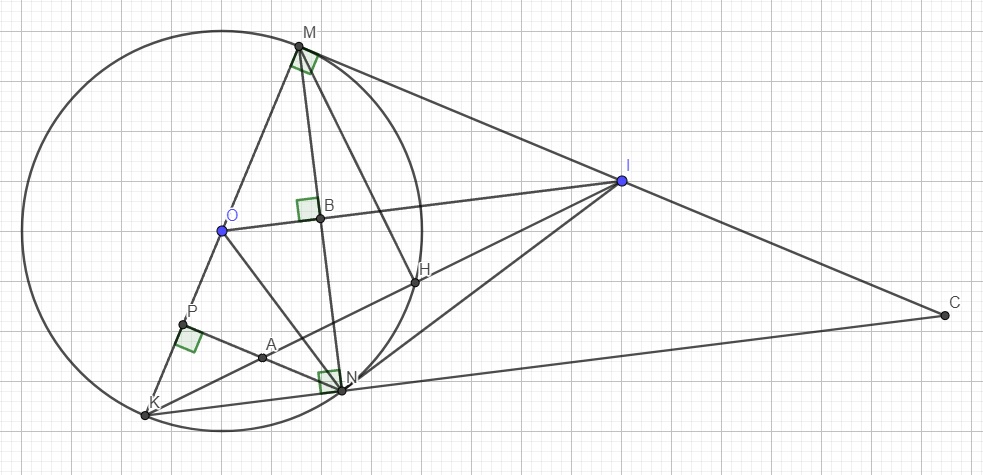
Do K đối xứng M qua O nên KM là 1 đường kính của (O)
Theo tính chất 2 tiếp tuyến cắt nhau, ta có \(IM=IN\) (1)
Xét hai tam giác IMH và IKM có:
\(\left\{{}\begin{matrix}\widehat{MIH}-chung\\\widehat{IMH}=\widehat{IKM}\left(\text{cùng chắn MH}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta IMH\sim\Delta IKM\left(g.g\right)\)
\(\Rightarrow\dfrac{IM}{IK}=\dfrac{IH}{IM}\Rightarrow IM^2=IH.IK\) (2)
(1);(2) \(\Rightarrow IM.IN=IH.IK\)
c.
Gọi A là giao điểm của IK và NP, B là giao điểm OI và MN
Nối NK kéo dài cắt MI tại C
Do \(IM=IN\) (cmt) và \(OM=ON=R\) \(\Rightarrow OI\) là trung trực của MN
\(\Rightarrow OI\perp MN\) tại B và B là trung điểm MN
Lại có KM là đường kính \(\Rightarrow\widehat{KNM}=90^0\) (góc nt chắn nửa đường tròn)
\(\Rightarrow OI||KC\) (cùng vuông góc MN)
Trong tam giác MKC, OI qua trung điểm O của cạnh bên KM và song song cạnh đáy KC
\(\Rightarrow OI\) là đường trung bình của tam giác MKC
\(\Rightarrow I\) là trung điểm MC \(\Rightarrow IM=IC\) (3)
Lại có \(NP||CM\) (cùng vuông góc KM), áp dụng định lý Thales:
\(\left\{{}\begin{matrix}\dfrac{AP}{IM}=\dfrac{KA}{KI}\\\dfrac{AN}{IC}=\dfrac{KA}{KI}\end{matrix}\right.\) \(\Rightarrow\dfrac{AP}{IM}=\dfrac{AN}{IC}\) (4)
(3);(4) \(\Rightarrow AP=AN\Rightarrow A\) là trung điểm NP
Hay đường thẳng IK đi qua trung điểm của NP





 Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 






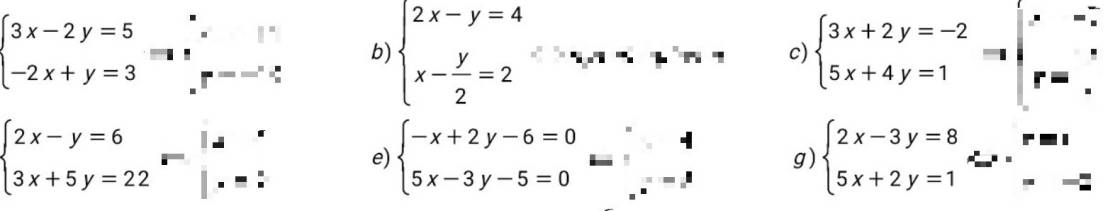
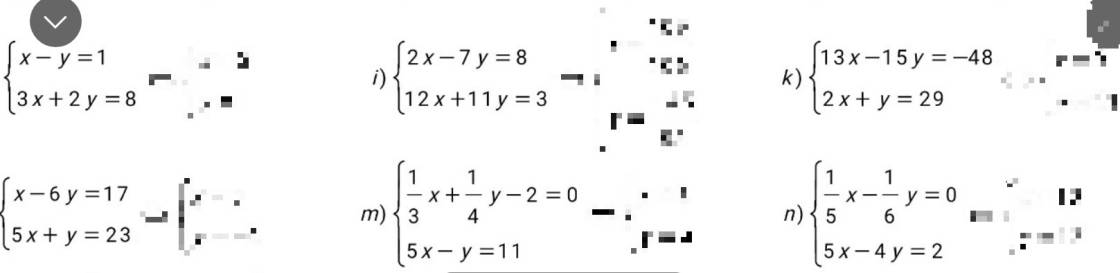 giúp mik với mik đg cần gấp
giúp mik với mik đg cần gấp