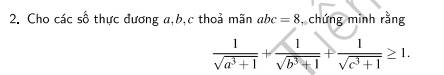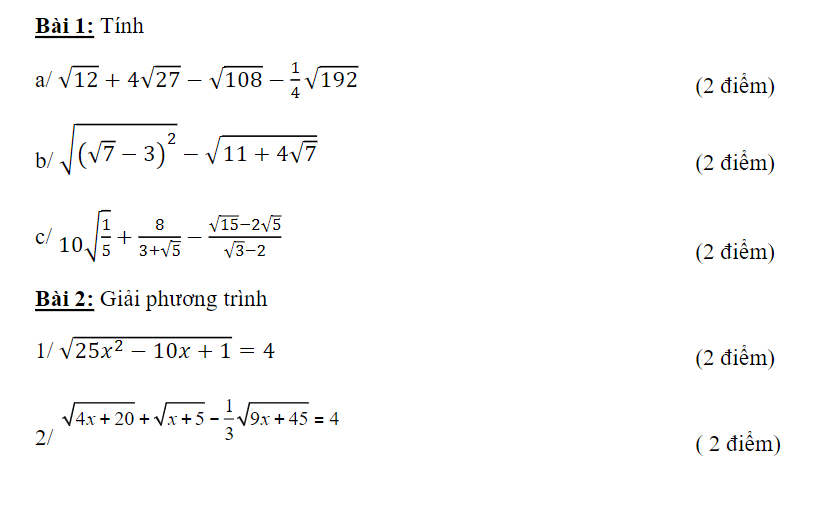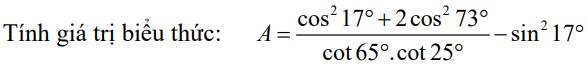Với `x > 0,x \ne 1,x \ne 4` có:
`(1/[\sqrt{x}-1]-1/\sqrt{x}):([\sqrt{x}+1]/[\sqrt{x}-2]-[\sqrt{x}+2]/[\sqrt{x}-1])`
`=[\sqrt{x}-\sqrt{x}+1]/[\sqrt{x}(\sqrt{x}-1)]:[(\sqrt{x}-1)(\sqrt{x}+1)-(\sqrt{x}+2)(\sqrt{x}-2)]/[(\sqrt{x}-2)(\sqrt{x}-1)]`
`=1/[\sqrt{x}(\sqrt{x}-1)].[(\sqrt{x}-2)(\sqrt{x}-1)]/[x-1-x+4]`
`=[\sqrt{x}-2]/[3\sqrt{x}]`
Đúng 0
Bình luận (0)
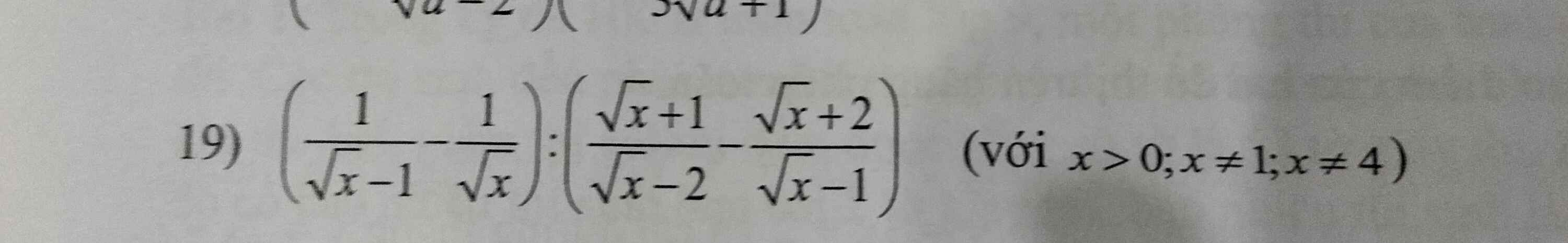
Mn giúp mik với,bh mik đang cần gấp lắm 19h30 mik phải có bài r nên mn giúp mik với 
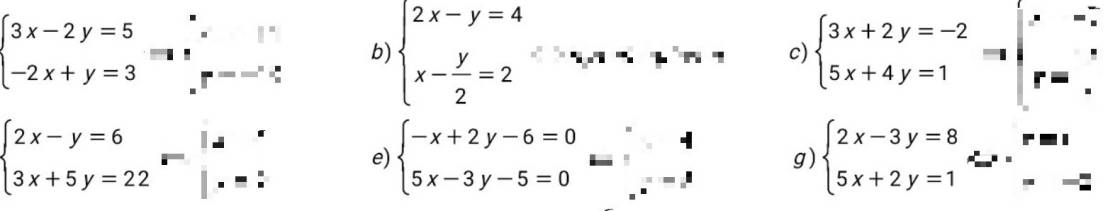
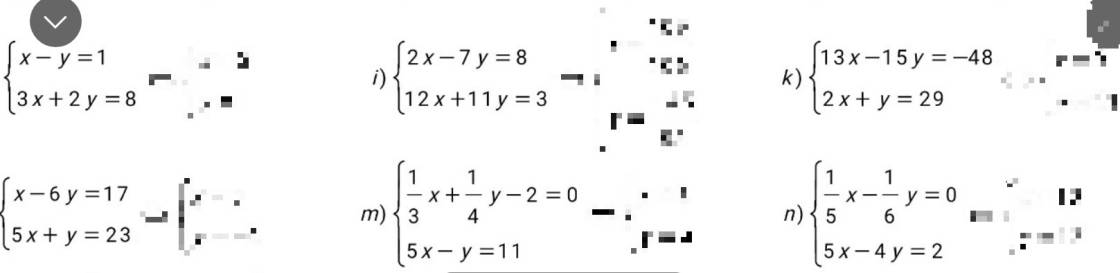giúp mik với mik đg cần gấp
