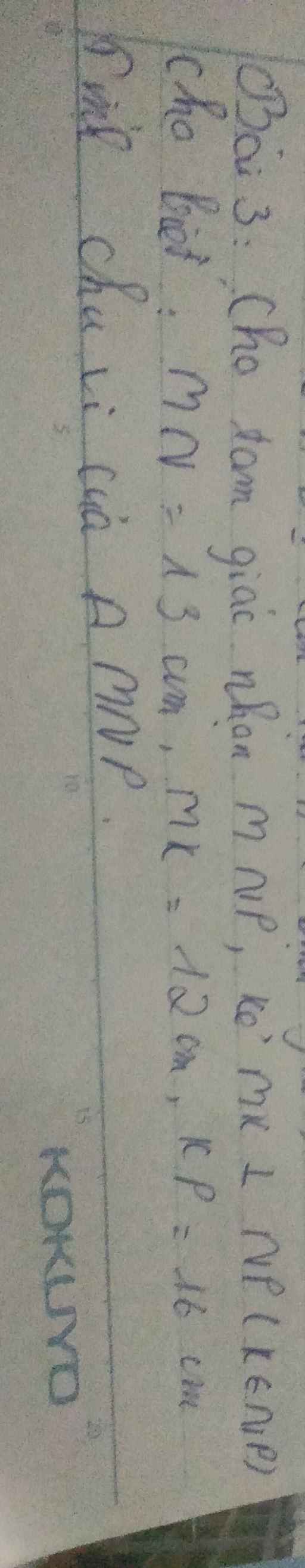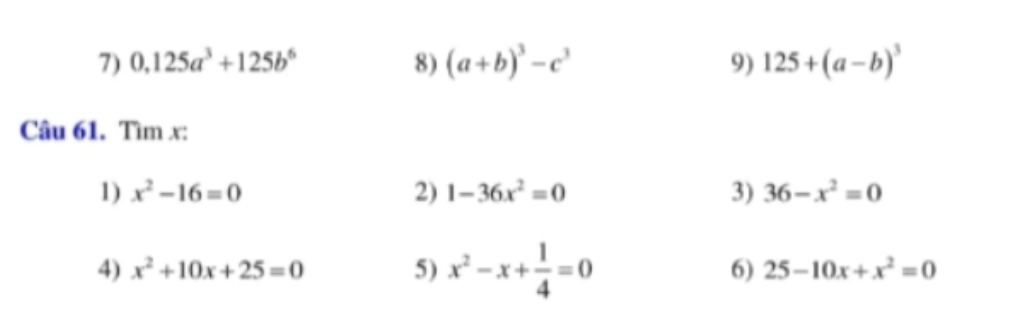giúp mik với ak
a: Xét ΔABC và ΔCDA có
\(\widehat{BAC}=\widehat{DCA}\)
AC chung
\(\widehat{ACB}=\widehat{CAD}\)
Do đó: ΔABC=ΔCDA
b: Xét ΔADB và ΔCBD có
AD=CB
AB=CD
BD chung
Do đó: ΔADB=ΔCBD
c: Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
Suy ra: Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường
=>OA=OC; OB=OD
Xét ΔAOB và ΔCOD có
OA=OC
\(\widehat{AOB}=\widehat{COD}\)
OB=OD
Do đó: ΔAOB=ΔCOD
Đúng 0
Bình luận (0)
