Giúp mik với ạ
Bài 2: Tính giá trị của mỗi biểu thức sau:
\[ M = \frac{6}{7} - \frac{6}{8} + \frac{6}{9} - \frac{6}{10} + \frac{6}{11} - \frac{6}{12} + \frac{6}{13} \]
\[ N = \frac{5}{12} + 1 - \frac{7}{11} \]
\[ P = \frac{3}{5} + \frac{3}{4} - \frac{3}{7} - \frac{3}{11} \]
Bài 3: Cho \( A = \frac{1}{3^2} + \frac{1}{4^2} + \ldots + \frac{1}{50^2} \) chứng tỏ rằng \( \frac{1}{4} < A < \frac{4}{9} \).
Bài 4: Tìm \( x, y \in \mathbb{Z} \), biết: \( \frac{1}{x} + \frac{y}{3} = \frac{5}{6} \).
Bài 5: Tìm số tự nhiên để \( \frac{n+3}{n+1} \) là số tự nhiên.
Bài 6: Cho \( A = \frac{1}{2} \cdot \frac{3}{4} \cdot \frac{5}{6} \cdot \ldots \cdot \frac{99}{100} \) CMR: \( A^2 < \frac{1}{101} \).
Bài 7: Chứng tỏ rằng: \( \frac{1}{4^3} + \frac{1}{5^3} + \frac{1}{6^3} + \ldots + \frac{1}{2014^3} < \frac{1}{3} \).
Bài 7: \(\frac{1}{4^2}<\frac{1}{3\cdot4}=\frac13-\frac14\)
\(\frac{1}{5^2}<\frac{1}{4\cdot5}=\frac14-\frac15\)
...
\(\frac{1}{2014^2}<\frac{1}{2013\cdot2014}=\frac{1}{2013}-\frac{1}{2024}\)
Do đó: \(\frac{1}{4^2}+\frac{1}{5^2}+\cdots+\frac{1}{2014^2}<\frac13-\frac14+\frac14-\frac15+\cdots+\frac{1}{2013}-\frac{1}{2014}=\frac13-\frac{1}{2014}<\frac13\)
Bài 5: Để \(\frac{n+3}{n+1}\) là số tự nhiên thì n+3⋮n+1
=>n+1+2⋮n+1
=>2⋮n+1
mà n+1>=1(do n là số tự nhiên)
nên n+1∈{1;2}
=>n∈{0;1}
















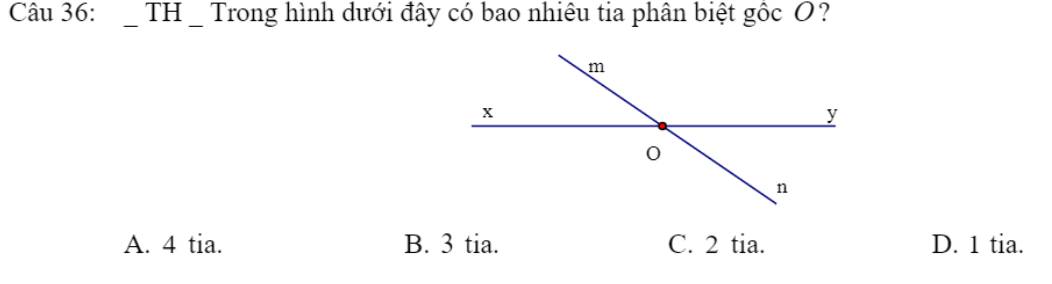

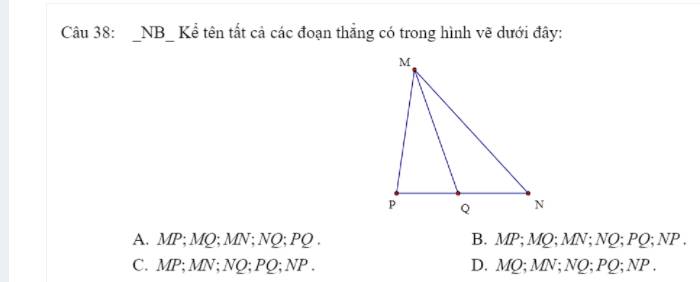

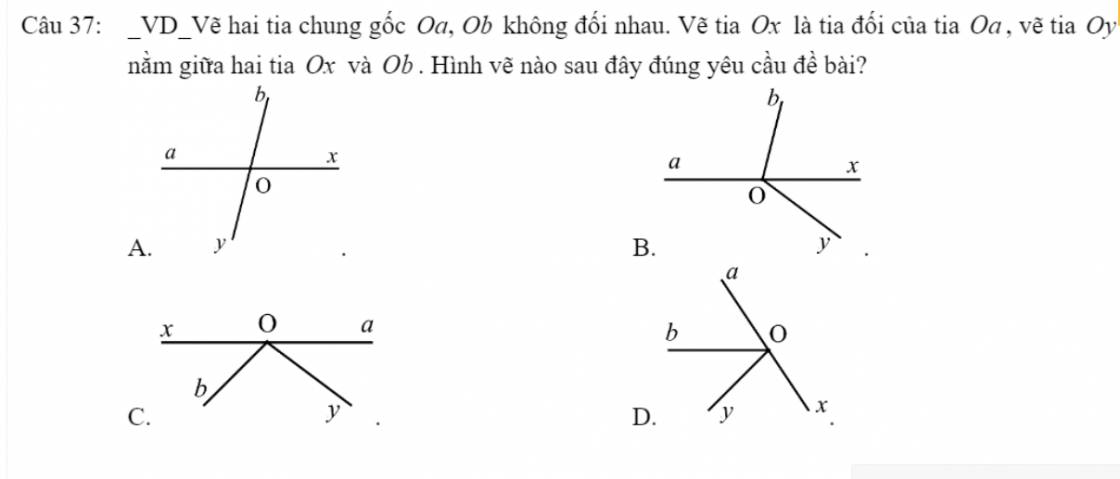
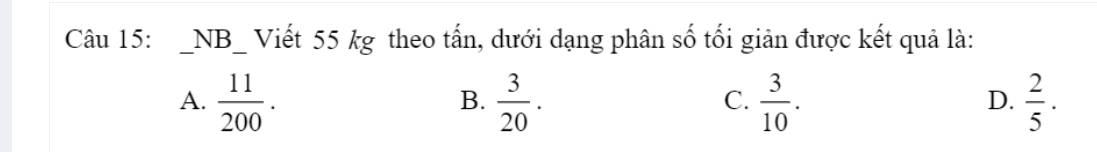 giúp mik với mik cần gấp ạ
giúp mik với mik cần gấp ạ