Bài 1:
$A=4+4^2+4^3+...+4^{23}+4^{24}$
$=(4+4^2)+(4^3+4^4)+....+(4^{23}+4^{24})$
$=4(1+4)+4^3(1+4)+....+4^{23}(1+4)$
$=4.5+4^3.5+...+4^{23}.5$
$=4.5(1+4^2+...+4^{22})=20(1+4^2+...+4^{22})\vdots 20$
Ta có đpcm
Đúng 0
Bình luận (2)
Bài 2:
$A=1+2+2^2+2^3+2^4+....+2^{99}+2^{100}$
$=1+(2+2^2)+(2^3+2^4)+...+(2^{99}+2^{100})$
$=1+2(1+2)+2^3(1+2)+...+2^{99}(1+2)$
$=1+2.3+2^3.3+...+2^{99}.3$
$=1+3(2+2^3+...+2^{99})$
Vậy $A$ chia $3$ dư $1$
Đúng 0
Bình luận (0)











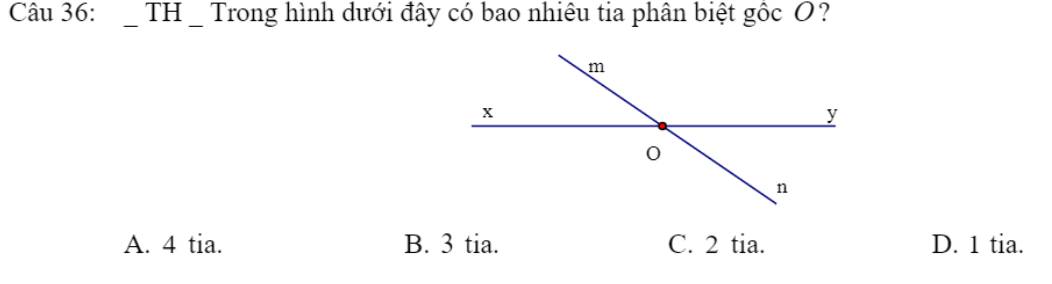

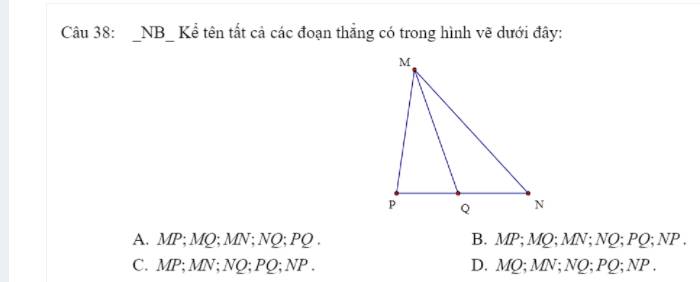

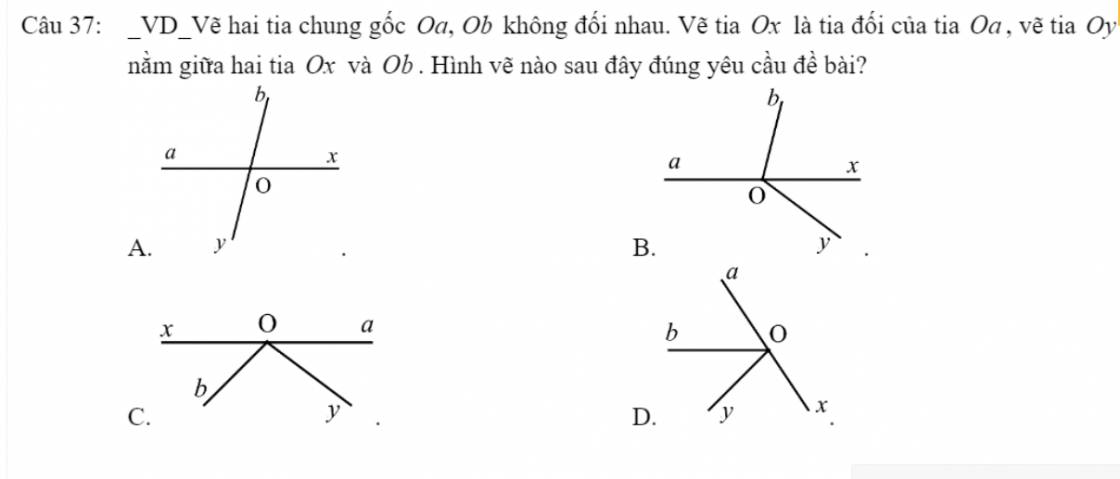
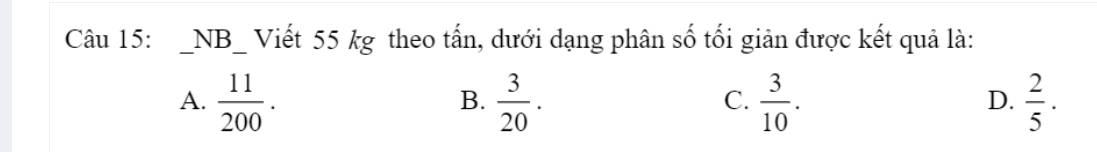 giúp mik với mik cần gấp ạ
giúp mik với mik cần gấp ạ