Câu 2:
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(y=\dfrac{x^2}{4}\) | \(1\) | \(\dfrac{1}{4}\) | \(0\) | \(1\) | \(\dfrac{1}{4}\) |
Đồ thị hàm số \(y=\dfrac{x^2}{4}\) là một Parabol đi qua các điểm A ( -2 ; 1 ) B ( -1 ; \(\dfrac{1}{4}\) ) O ( 0 ; 0 ) B' ( 1 ; \(\dfrac{1}{4}\) ) A' ( 2 ; \(\dfrac{1}{4}\) )
Đồ thị hàm số \(y=\dfrac{1}{2}x+2\)
Cho x = 1 ⇒ y = \(\dfrac{5}{2}\) ta có: M ( 0 ; \(\dfrac{5}{2}\) )
Cho y = 1 ⇒ x = -2 ta có: N ( -2 ; 0 )
Đồ thị hàm số \(y=\dfrac{1}{2}x+2\) là một đường thẳng đi qua các điểm M ( 0 ; \(\dfrac{5}{2}\) ) và N ( - 2 ; 0 )
Vẽ đồ thị tự vẽ nha
b) Phương trình hoành độ giao điểm của ( P ) và ( D ) ta có:
\(\dfrac{x^2}{4}=\dfrac{1}{2}x+2\)
\(\Leftrightarrow x^2-2x-8=0\)
Ta có: △ = b2 - 4ac = ( -2 )2 - 4 . 1 . ( - 8 ) = 36
Vì △ = 36 > 0 ⇒ Phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-\left(-2\right)+\sqrt{36}}{2.2}=4\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-\left(-2\right)-\sqrt{36}}{2.1}=-2\)
Với x = 4 ⇒ y = 4 ta có ( x ; y ) = ( 4 ; 4 )
Với x = - 2 ⇒ y = 1 ta có ( x ; y ) = ( -2 ; 1 )
Vậy tại ( 4 ; 4 ) và ( -2 ; 1 ) thì ( P ) và ( D ) giao nhau
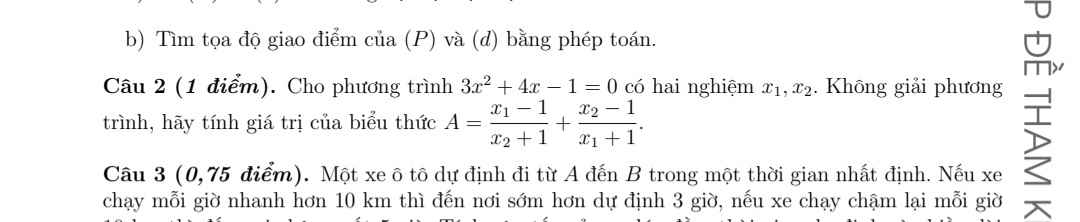
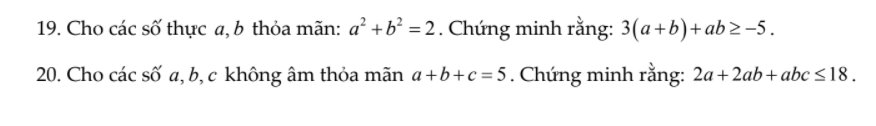
Giúp mik câu 3 bài 1 với ạ
