\(10,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow x^2+8+x^2+3-2\sqrt{\left(x^2+8\right)\left(x^2+3\right)}=4x^2-4x+1\\ \Leftrightarrow-2\sqrt{x^4+11x^2+24}=2x^2-4x-10\\ \Leftrightarrow-\sqrt{x^4+11x^2+24}=x^2-2x-5\\ \Leftrightarrow x^4+11x^2+24=\left(x^2-2x-5\right)^2\\ \Leftrightarrow x^4+11x^2+24=x^4+4x^2+25-4x^3+20x-10x^2\\ \Leftrightarrow4x^3+17x^2-20x-1=0\\ \Leftrightarrow4x^3-4x^2+21x^2-21x+x-1=0\\ \Leftrightarrow\left(x-1\right)\left(4x^2+21x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\4x^2+21x+1=0\left(1\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{-21+5\sqrt{17}}{8}\\x=\dfrac{-21-5\sqrt{17}}{8}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Mọi người giúp mik câu 10 với! Mik cảm ơn nhiều !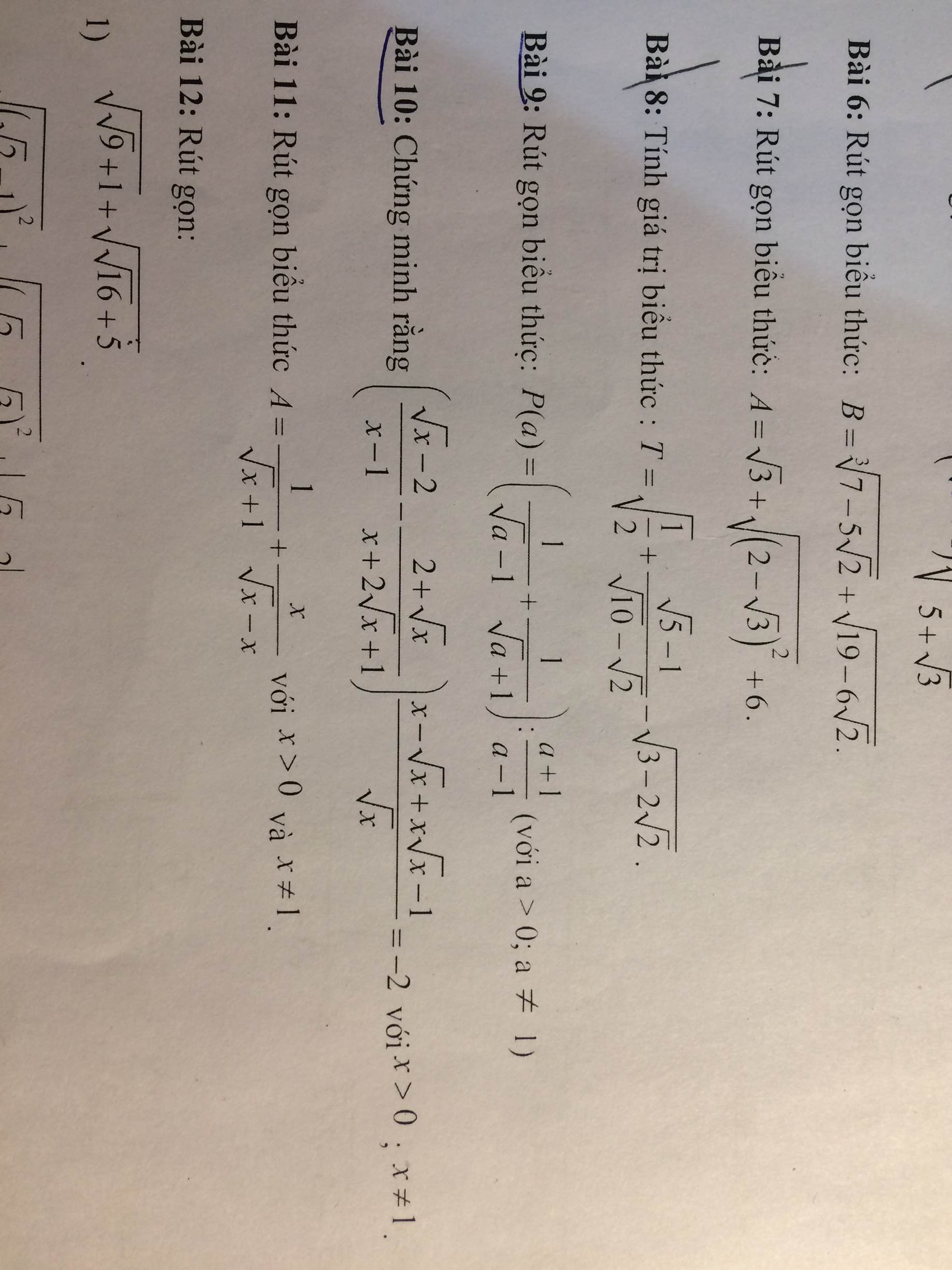
Cần gấp nha giúp giùm mik với, đừng làm quá tắt hum hỉu CẦN CÂU C THÔI

M.n giúp mik câu k vs e nha ..:33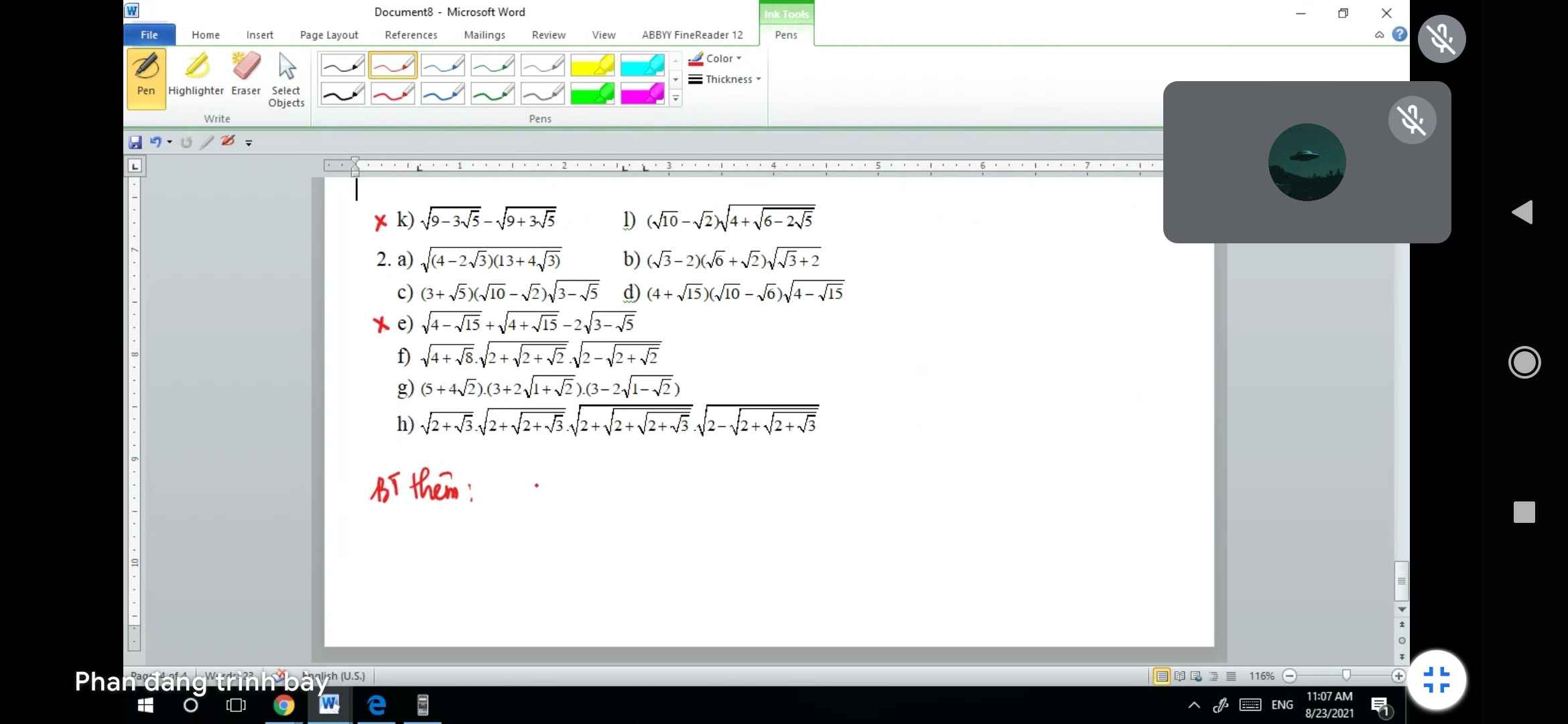
CỨU MỌI NGƯỜI ƠI MIK PHẢI NỘP LUN RỒI Bài 12, Cho đường thẳng (d) có phương trình 2(m-1)x+(m-2)y2 cC )Tim m để (d) cách gốc tọa độ một khoảng lớn nhất.giúp mik câu C với ĐÂY LÀ GỢI Ý MỌI NGƯỜI LÀM GIÚP MIK VỚI NHÉ MIK CẢM ƠN Ạ ( GIẢI THEO TOÁN 9 GIÚP MIK Ạ ) MIK ĐANG CẦN GẤP XIN MỌI NGƯỜI GIÚP MIK ĐẤY ẠBài 12c - Kẻ OH vuông góc với (d), H thuộc (d)- Xét m2 tìm OH - Khi m khác 2, chuyển (d) về dạng y ax+b - Có OHOM - Dấu bằng xảy ra khi OHOM (H trùng M). Khi đó OM vuông góc với (d) - Viết pt đườn...
Đọc tiếp
CỨU MỌI NGƯỜI ƠI MIK PHẢI NỘP LUN RỒI
Bài 12, Cho đường thẳng (d) có phương trình 2(m-1)x+(m-2)y=2 c
C )Tim m để (d) cách gốc tọa độ một khoảng lớn nhất.
giúp mik câu C với ĐÂY LÀ GỢI Ý MỌI NGƯỜI LÀM GIÚP MIK VỚI NHÉ MIK CẢM ƠN Ạ ( GIẢI THEO TOÁN 9 GIÚP MIK Ạ ) MIK ĐANG CẦN GẤP XIN MỌI NGƯỜI GIÚP MIK ĐẤY Ạ
Bài 12c - Kẻ OH vuông góc với (d), H thuộc (d)
- Xét m=2 tìm OH
- Khi m khác 2, chuyển (d) về dạng y= ax+b
- Có OH<=OM
- Dấu bằng xảy ra khi OH=OM (H trùng M).
Khi đó OM vuông góc với (d)
- Viết pt đường thẳng OM -
Điều kiện OM vuông góc với d => m=?
- Tính OM=? (Áp dụng công thức)
Kết luận:.lớn nhất OH=OM=?, với m=?
Bài 12, Cho đường thẳng (d) có phương trình 2(m-1)x+(m-2)y2a) Vẽ (d) với m1/2b) Cmr: (d) lun đi qua một điềm cố định với mọi m.c) Tim m để (d) cách gốc tọa độ một khoảng lớn nhất.giúp mik câu C với ĐÂY LÀ GỢI Ý MỌI NGƯỜI LÀM GIÚP MIK VỚI NHÉ MIK CẢM ƠN Ạ ( GIẢI THEO TOÁN 9 GIÚP MIK Ạ ) MIK ĐANG CẦN GẤP XIN MỌI NGƯỜI GIÚP MIK ĐẤY ẠBài 12c - Kẻ OH vuông góc với (d), H thuộc (d)- Xét m2 tìm OH- Khi m khác 2, chuyển (d) về dạng y ax+b- Có OHOM - Dấu bằng xảy ra khi OHOM (H trùng M).Khi đó OM vuông g...
Đọc tiếp
Bài 12, Cho đường thẳng (d) có phương trình 2(m-1)x+(m-2)y=2
a) Vẽ (d) với m=1/2
b) Cmr: (d) lun đi qua một điềm cố định với mọi m.
c) Tim m để (d) cách gốc tọa độ một khoảng lớn nhất.
giúp mik câu C với ĐÂY LÀ GỢI Ý MỌI NGƯỜI LÀM GIÚP MIK VỚI NHÉ MIK CẢM ƠN Ạ ( GIẢI THEO TOÁN 9 GIÚP MIK Ạ ) MIK ĐANG CẦN GẤP XIN MỌI NGƯỜI GIÚP MIK ĐẤY Ạ
Bài 12c - Kẻ OH vuông góc với (d), H thuộc (d)
- Xét m=2 tìm OH
- Khi m khác 2, chuyển (d) về dạng y= ax+b
- Có OH<=OM - Dấu bằng xảy ra khi OH=OM (H trùng M).
Khi đó OM vuông góc với (d)
- Viết pt đường thẳng OM
- Điều kiện OM vuông góc với d => m=?
- Tính OM=? (Áp dụng công thức)
Kết luận:.lớn nhất OH=OM=?, với m=?
Bài 12, Cho đường thẳng (d) có phương trình 2(m-1)x+(m-2)y2a) Vẽ (d) với m1/2b) Cmr: (d) lun đi qua một điềm cố định với mọi m.c) Tim m để (d) cách gốc tọa độ một khoảng lớn nhất.giúp mik câu C với ĐÂY LÀ GỢI Ý MỌI NGƯỜI LÀM GIÚP MIK VỚI NHÉ MIK CẢM ƠN Ạ ( GIẢI THEO TOÁN 9 GIÚP MIK Ạ ) MIK ĐANG CẦN GẤP XIN MỌI NGƯỜI GIÚP MIK ĐẤY ẠBài 12c - Kẻ OH vuông góc với (d), H thuộc (d) - Xét m2 tìm OH - Khi m khác 2, chuyển (d) về dạng y ax+b - Có OHOM - Dấu bằng xảy ra khi OHOM (H trùng M). Khi đó OM vuô...
Đọc tiếp
Bài 12, Cho đường thẳng (d) có phương trình 2(m-1)x+(m-2)y=2
a) Vẽ (d) với m=1/2
b) Cmr: (d) lun đi qua một điềm cố định với mọi m.
c) Tim m để (d) cách gốc tọa độ một khoảng lớn nhất.
giúp mik câu C với ĐÂY LÀ GỢI Ý MỌI NGƯỜI LÀM GIÚP MIK VỚI NHÉ MIK CẢM ƠN Ạ ( GIẢI THEO TOÁN 9 GIÚP MIK Ạ ) MIK ĐANG CẦN GẤP XIN MỌI NGƯỜI GIÚP MIK ĐẤY Ạ
Bài 12c - Kẻ OH vuông góc với (d), H thuộc (d)
- Xét m=2 tìm OH
- Khi m khác 2, chuyển (d) về dạng y= ax+b
- Có OH<=OM - Dấu bằng xảy ra khi OH=OM (H trùng M).
Khi đó OM vuông góc với (d)
- Viết pt đường thẳng OM
- Điều kiện OM vuông góc với d => m=?
- Tính OM=? (Áp dụng công thức)
Kết luận:.lớn nhất OH=OM=?, với m=?
Mọi người ơi giúp mik câu này với ạ, mik đg cần gâp cho mik câu trả lời chi tiết ko tắt bước nhất với ạ,xong mik sẽ tick mik cảm ơn !

giúp mik câu b
giải ra đc đáp án là sắp xỉ 364 000 đồng là đúng nha
Rút gọn :\(\sqrt{12-2.\sqrt{35}}\)
giúp mik nha!!!


 Giúp mik câu 10 , 12 với nha
Giúp mik câu 10 , 12 với nha









