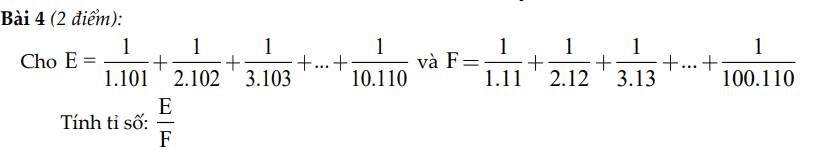\(E=\frac{1}{1\cdot101}+\frac{1}{2\cdot102}+\cdots+\frac{1}{10\cdot110}\)
\(=\frac{1}{100}\left(\frac{100}{1\cdot101}+\frac{100}{2\cdot102}+\cdots+\frac{100}{10\cdot110}\right)\)
\(=\frac{1}{100}\left(1-\frac{1}{101}+\frac12-\frac{1}{102}+\cdots+\frac{1}{10}-\frac{1}{110}\right)\)
\(=\frac{1}{100}\left(1+\frac12+\cdots+\frac{1}{10}-\frac{1}{101}-\frac{1}{102}-\cdots-\frac{1}{110}\right)\)
\(F=\frac{1}{1\cdot11}+\frac{1}{2\cdot12}+\frac{1}{3\cdot13}+\cdots+\frac{1}{100\cdot110}\)
\(=\frac{1}{10}\left(\frac{10}{1\cdot11}+\frac{10}{2\cdot12}+\cdots+\frac{10}{100\cdot110}\right)\)
\(=\frac{1}{10}\left(1-\frac{1}{11}+\frac12-\frac{1}{12}+\cdots+\frac{1}{100}-\frac{1}{110}\right)\)
\(=\frac{1}{10}\left(1+\frac12+\cdots+\frac{1}{10}-\frac{1}{101}-\frac{1}{102}-\cdots-\frac{1}{110}\right)\)
Do đó: \(\frac{E}{F}=\frac{1}{100}:\frac{1}{10}=\frac{10}{100}=\frac{1}{10}\)