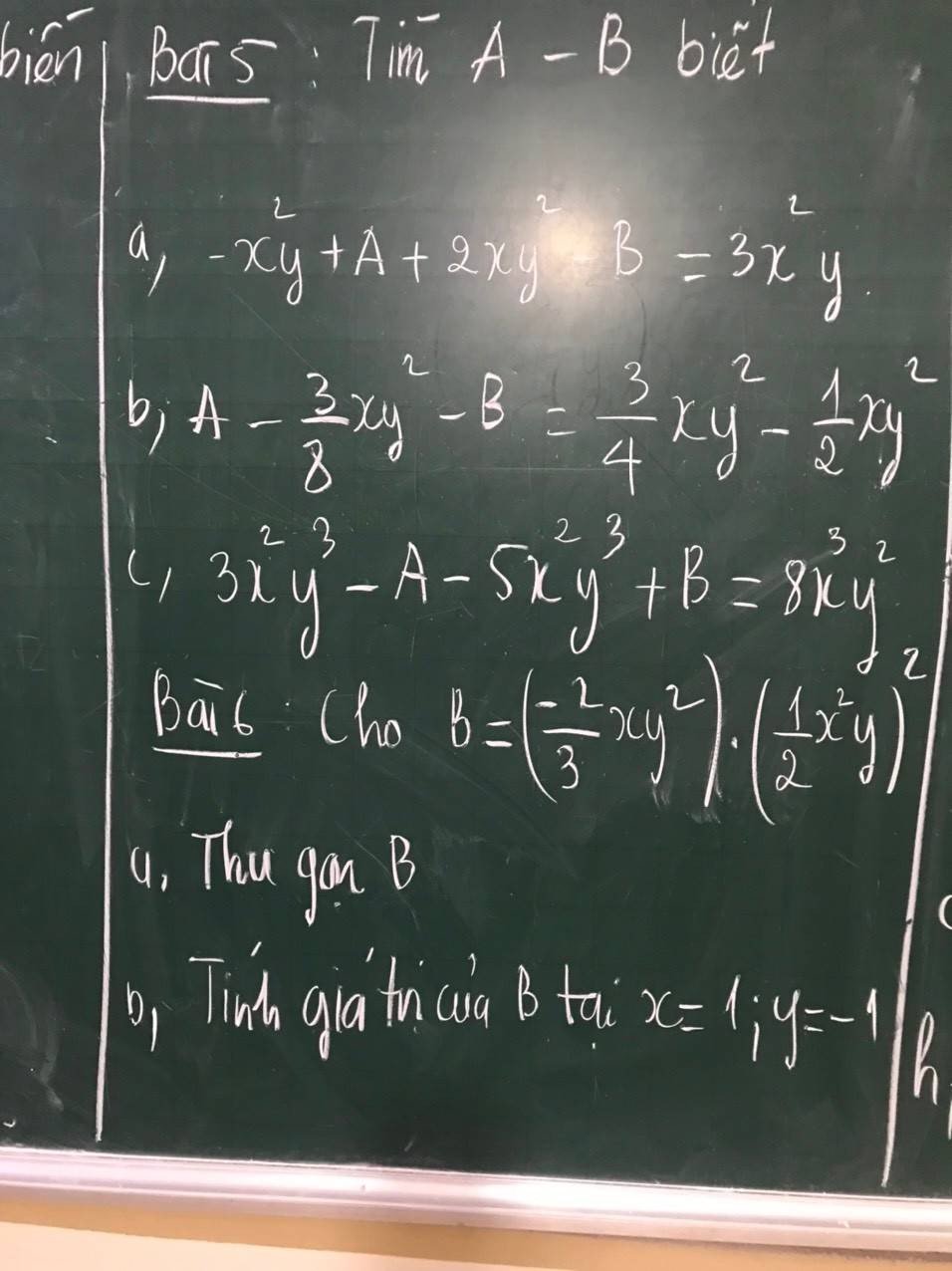Question

  giúp mik bài 20;21;23;25;26 đc ko🙏

 

Answer 1

Hướng dẫn rồi em giải theo hướng đó:

20. Đặt \(\left\{{}\begin{matrix}4a+5=m^2\\a+3=n^2\end{matrix}\right.\) với m, n là số tự nhiên

\(\Rightarrow4n^2-m^2-4\left(a+3\right)-\left(4a+5\right)\)

\(\Leftrightarrow\left(2n-m\right)\left(2n+m\right)=7\)

Tới đây lập bảng ước số tìm ra m; n từ đó tìm ra a

21.

\(n^2+3n+2=\left(n+1\right)\left(n+2\right)\) có ít nhất 2 ước nguyên nên nó là SNT khi và chỉ khi:

\(\left\{{}\begin{matrix}n+1=1\\n+2\text{ là số nguyên tố}\end{matrix}\right.\) \(\Rightarrow n=0\)

23. Đặt \(p+1=n^2\) (với n tự nhiên và \(n\ge1\))

\(\Rightarrow p=\left(n-1\right)\left(n+1\right)\) \(\Rightarrow p\)  có ít nhất 2 ước nguyên

Mà p nguyên tố \(\Rightarrow\left\{{}\begin{matrix}n-1=1\\n+1\text{ là số nguyên tố}\end{matrix}\right.\) \(\Rightarrow n=2\)

\(\Rightarrow p=3\)

Answer 2

25.

\(\dfrac{n^2+n+1}{n+2}\in Z\Rightarrow n-1+\dfrac{3}{n+2}\in Z\)

\(\Rightarrow n+2=Ư\left(3\right)\Rightarrow n=...\)

b.

\(\dfrac{n^3+2n^2-3n+2}{n^2-n}\in Z\Rightarrow n+3+\dfrac{2}{n^2-n}\in Z\)

\(\Rightarrow n^2-n=Ư\left(3\right)\)

\(\Rightarrow...\)

c.

\(\dfrac{2n^2+2n-1}{2n+1}\Rightarrow\dfrac{4n^2+4n-2}{2n+1}\in Z\Rightarrow2n+1-\dfrac{3}{2n+1}\in Z\)

\(\Rightarrow2n+1=Ư\left(3\right)\)

\(\Rightarrow n=...\)

(Trường hợp này tìm ra n xong phải thế ngược lại để kiểm tra)

Answer 3

26.

a.

Đặt \(P=\dfrac{n+2}{n^2+2}\)

Ta có: \(P-2=\dfrac{n+2}{n^2+2}-2=\dfrac{-2n^2+n-2}{n^2+2}=\dfrac{-2\left(n-\dfrac{1}{4}\right)^2-\dfrac{15}{8}}{n^2+2}< 0\)

\(\Rightarrow P< 2\)

\(P+1=\dfrac{n+2}{n^2+2}+1=\dfrac{n^2+n+4}{n^2+2}=\dfrac{\left(n+\dfrac{1}{2}\right)^2+\dfrac{15}{4}}{n^2+2}>0\)

\(\Rightarrow P>-1\)

\(\Rightarrow-1< P< 2\) mà \(P\in Z\Rightarrow\left[{}\begin{matrix}P=0\\P=1\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}\dfrac{n+2}{n^2+2}=0\\\dfrac{n+2}{n^2+2}=1\end{matrix}\right.\) \(\Rightarrow...\)

Answer 4

26b.

\(\dfrac{n^3-3n^2-2n-3}{n^2+n+1}\in Z\Rightarrow n-4+\dfrac{n+1}{n^2+n+1}\in Z\)

\(\Rightarrow\dfrac{n+1}{n^2+n+1}\in Z\)

Đặt \(P=\dfrac{n+1}{n^2+n+1}\)

Ta có: \(P=\dfrac{n^2+n+1-n^2}{n^2+n+1}=1-\dfrac{n^2}{n^2+n+1}\le1\)

\(P=\dfrac{3n+3}{3\left(n^2+n+1\right)}=\dfrac{-\left(n^2+n+1\right)+n^2+4n+4}{3\left(n^2+n+1\right)}=-\dfrac{1}{3}+\dfrac{\left(n+2\right)^2}{3\left[\left(n+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\right]}\ge-\dfrac{1}{3}\)

\(\Rightarrow-\dfrac{1}{3}\le P\le0\)

Mà \(P\in Z\Rightarrow P=0\)

\(\Rightarrow\dfrac{n+1}{n^2+n+1}=0\Rightarrow n=...\)